Всем известно, что в РАУЗ применяется метод решения систем линейных уравнений для расчета себестоимости. Чтобы понять, откуда лезут миллиарды триллионов оборотов, для начала разберемся в том, как же решается СЛАУ. Рассмотрим это на примере, очень идеальном, чтобы понять суть уравнения, идеальном и кривом, и попытаемся сделать выводы.
Для начала необходимо себе в голове представить граф направлений движений ТМЗ (рассматривать расчет себестоимости тут не буду, для этого надо писать отдельную статью). Как известно, в графах у нас есть вершины и дуги. Для нашей прикладной задачи граф у нас будет направленный. Вершины графа есть узлы, которые идентифицируются номенклатурой на складе (Ключ аналитики вида учета + Ключ аналитики вида затрат).
Система решения алгебраических уравнений помогает найти решения для больших объемов данных с меньшими затратами на вычисление.
Общая система уравнений в скалярном виде выглядит следующим образом:

Стоимость товара на складе равна стоимости, полученной извне (например, при покупке товара) плюс начальный остаток плюс стоимость товара, перемещенного с других складов, умноженная на количество перемещенного товара.
Решается система методом простых итераций (Якоби). Уравнение приводится к виду:
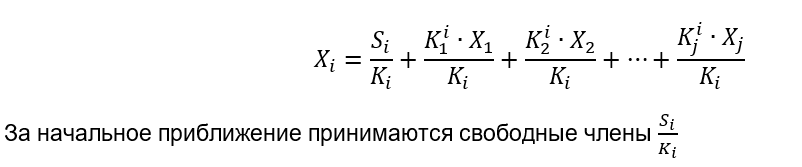
Для начала возьмем самый идеальный пример, когда у нас стоимость во всех узлах одинаковая, как на начало, так и в движениях. Т.е., не решая систему, у нас левые и правые части уравнений должны сойтись.
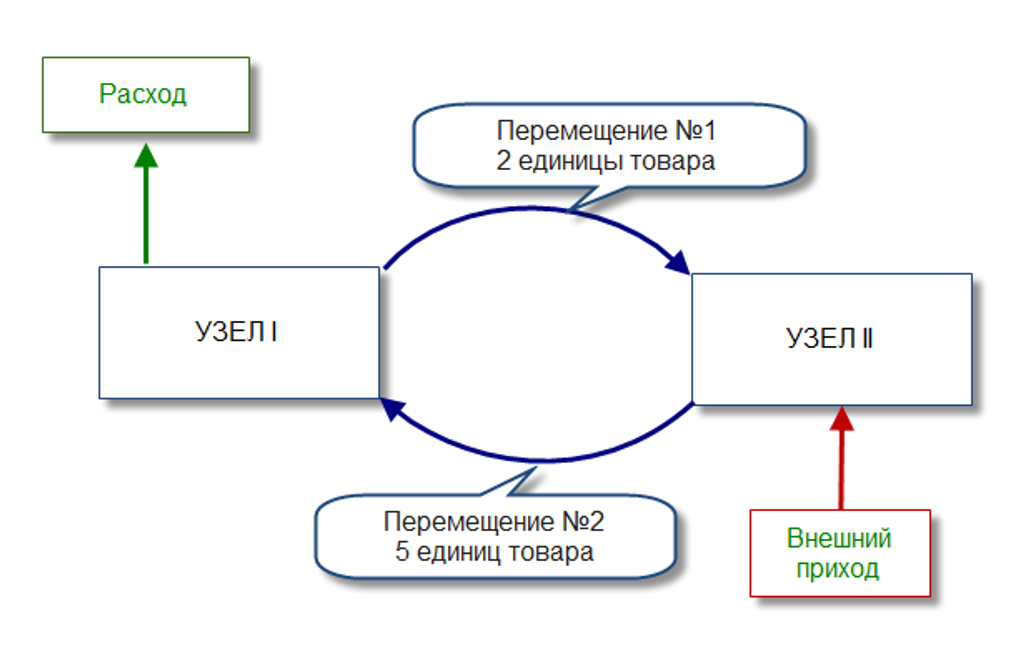
Пример 1. Пусть у нас дана только одна номенклатура и два склада. Номенклатура Товар 1 на складе 1 – первый узел (I), номенклатура Товар 1 на складе 2 – второй узел (II).
Граф движения ТМЗ:
В
Начальные условия:
Начальные остатки:
Узел I — 10 шт. стоимостью 1000 р.
Узел I — 10 шт. стоимостью 1000 р.
Перемещения:
Перемещение №1 2 шт. стоимостью 200р.
Перемещение №2 5 шт. стоимостью 500р.
Внешний приход не рассматриваем. Вся стоимость одинаковая, поэтому, подставив значения, в системе мы должны получить равенство левой и правой части.
Для нашего примера система будет иметь следующий общий вид:
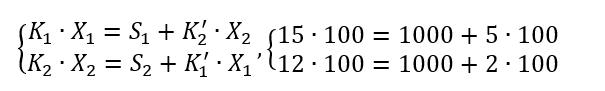
Данный пример демонстрирует, из чего у нас получилась такая СЛАУ.
Пример 2. Теперь к примеру 1 добавим внешнее поступление 5 шт. стоимостью 550р. Остальные начальные условия остаются те же самые.
Т.к. мы не знаем точную стоимость, и ее нам надо найти, решив систему, то стоимость в системе оставим как неизвестную:
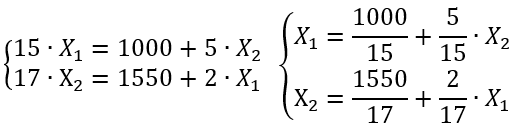
В качестве начального приближения возьмем:
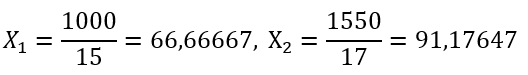
Итерация 1:

Итерация 2:
В качестве значений неизвестных берем значения, найденные на первой итерации:
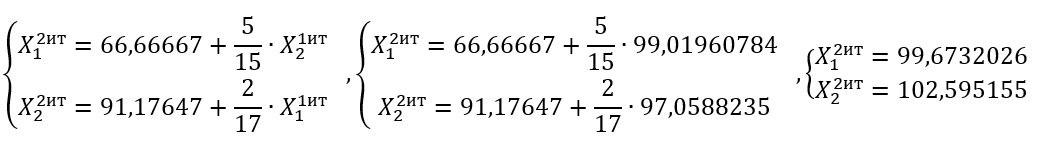
И так далее рассчитываем до получения нужной точности в Excel:
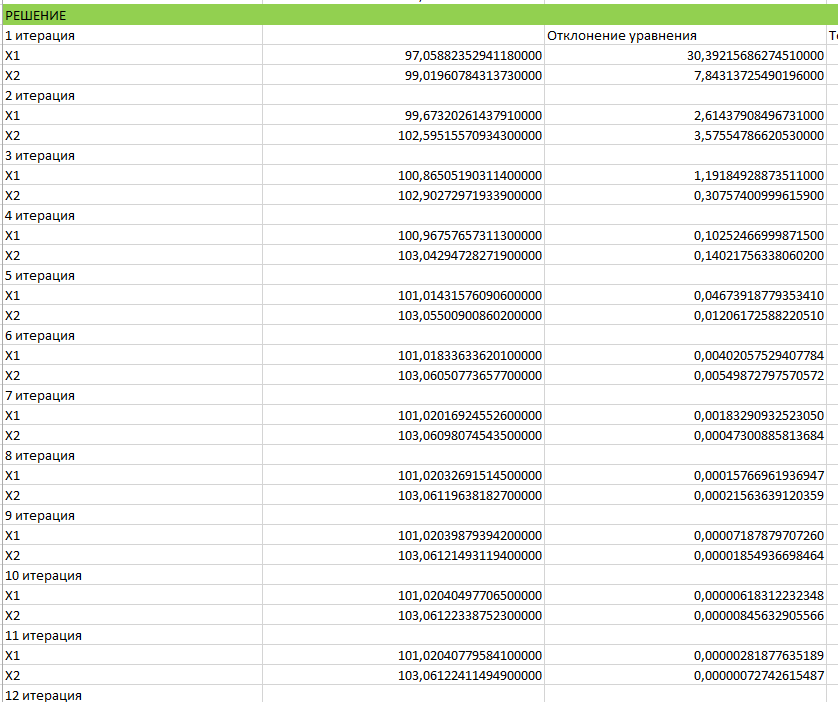
В
Тут хотелось бы обратить внимание на одно правило сходимости метода решения СЛАУ.
Нашу СЛАУ можно представить в следующем виде:
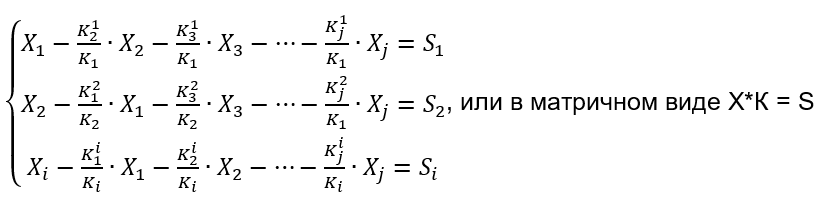
Так вот метод Якоби сходится, если выполняется условие что норма матрицы К<1, если норма превышает 1, то есть вероятность, что решение не сойдется.
Для нашего примера норма рассчитывается по формуле:
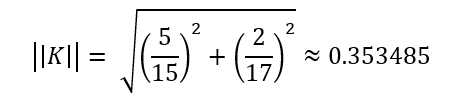
Пример 3, когда решение не сходится.
Решение может не сходиться в том случае, если у нас на каком-либо узле графа начальный остаток и весь приход по модулю меньше, чем приход по перемещениям, в этом случае норма матрицы K становится больше единицы.
Начальные условия:
Начальные остатки:
Узел I — -2,523 шт. стоимостью 8262,4 р.
Узел I – 8,656 шт. стоимостью 29765,3 р.
Перемещения:
Перемещение №1 2,29 шт. стоимостью 0р.
Перемещение №2 2,25 шт. стоимостью 0р.
Внешний приход отсутствует
В данном случае:
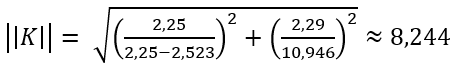
И решение выглядит следующим образом:
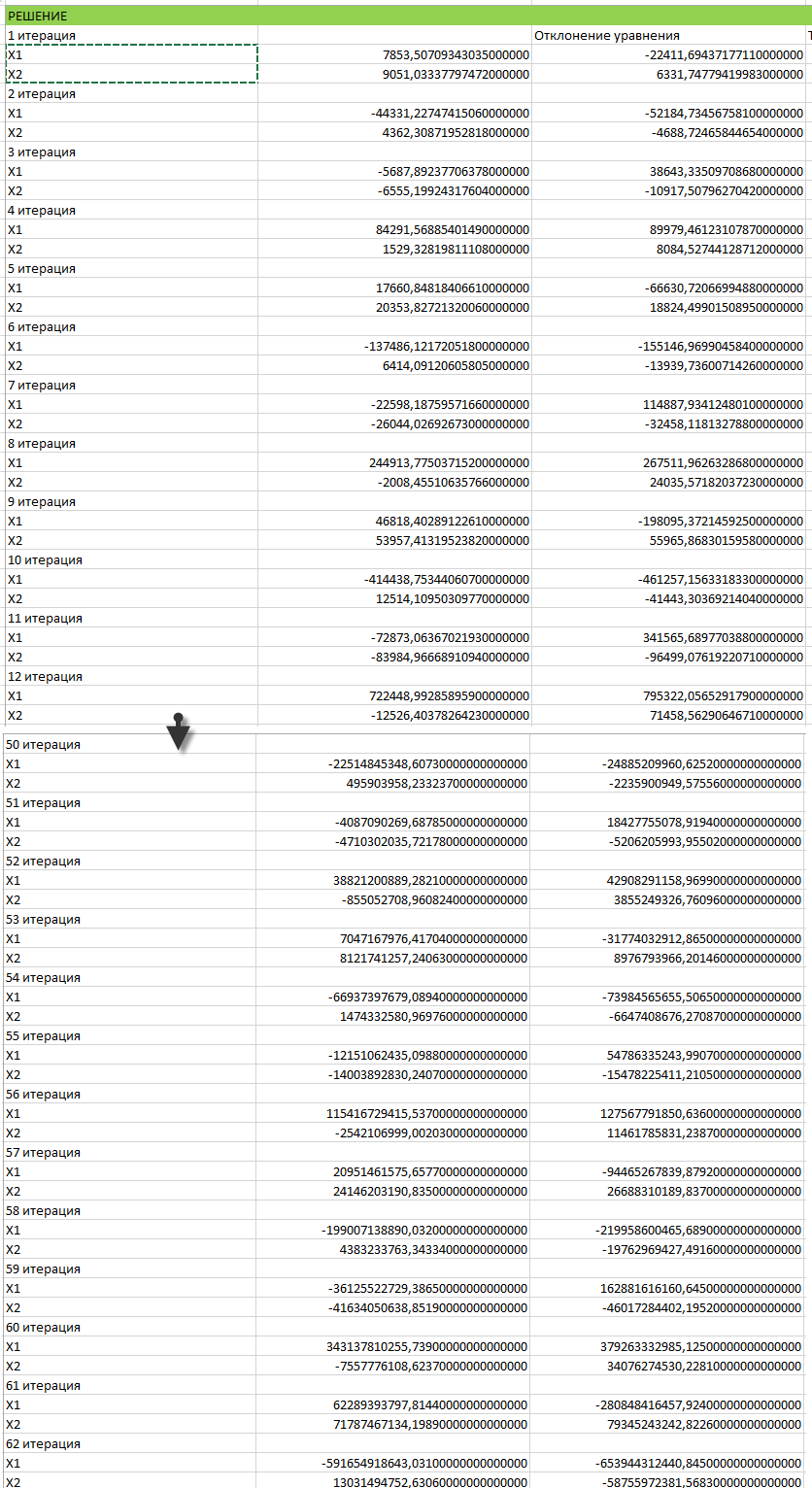
Т.е. чем больше результат, тем больше становится отклонение, а оно должно уменьшаться.
Файл Excel, в котором эти примеры рассчитаны, прилагается.






Это означает, что будет ошибка и
Программа посчитает не правильно себестоимость такого товара?
(1) script,
Я, опытным путем, пробовал разные варианты для данного условия и в некоторых случаях решение было найдено, в некоторых нет. Однозначно сказать могу только что решение 100% будет найдено если норма меньше единицы. Если же она больше единицы, то есть вероятность что решение не будет найдено.
Надеюсь что с помощью данной статьи кто-то из сообщества или общими усилиями поможет однозначно разобраться и понять данную ситуацию и конкретизировать правило при котором решения СЛАУ не будет.
УПП начинает дурить выводя Милиадры в сумму -/+ при не корректном учете, в честности минусовых остатках. Когда есть два документа с одинаковым временем и МПЗ.
Это происходит при учет «Стоимости по Среднему» с «По прямым затратам».
Тут можно выбрать по «Плановым» или «Нулевым» ну или восстанавливать последовательность документов и убирать минусы.
(3) Константин С.,
Из решения системы видно, что оно ни как не зависит от выбранного вами способа расчета стоимости при движении ТМЗ. Эти стоимости как раз в уравнениях являются неизвестными, а в качестве свободных членов уравнения принимается стоимость начального остатка и стоимость внешнего прихода.
На счет кривизны учета тут можно долго спорить и рассуждать, в жизни допустимо (особенно для больших торговых сетях) наличие отрицательных остатков, т.к. возникают ошибки в пересортицах и до момента инвентаризации они не могут быть исправлены, а инвентаризацию делать ежемесячно перед закрытием не каждый может.
(4) да ладно. При других способах просто не будет данных цифр.
(5) Константин С., Указанный пример в статье взят из базы, где расчет стояли как раз по плановым ценам.
Разгребать минуса в сети магазинов с 50 тыс. товарными позициями по месяцам?