В этой статье я хочу показать различные подходы к решению классической игры Змейка (Источник идеи статьи). Думаю, правила и цель игры всем известны.
1. Кратчайший путь. Поиск в ширину (Breadth-first search) Вики
Представим поле игры в виде графа. Каждая ячейка поля связана как минимум с 2-мя соседями. Таким образом, перебирая соседей можно найти ячейку с "едой". А после восстановить путь по которому мы до нее дошли.
Поиск в ширину — один из методов обхода графа. Заключается в том, что сначала рассматриваются все подчиненные узлы одного уровня, а после все подчиненные подчиненных и т.д. Под узлом понимается адрес ячейки со ссылкой на "Родителя" (ячейку через которую мы добрались до узла).
Примерный алгоритм действий:
- Создать пустой стек и поместить в него узел-источник
- Пока стек не пустой извлекать по одному узлу с вершины стека
- Проверить не является ли текущий узел целевым. Если да, то завершить поиск.
- Перебрать все подчиненные узлы, которые еще не были просмотрены. Добавить их в конец стека и пометить как просмотренные.
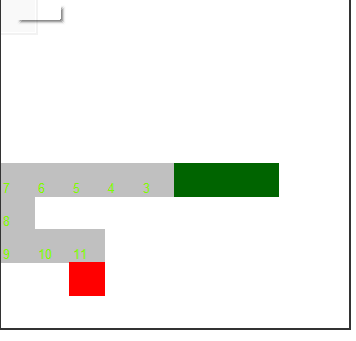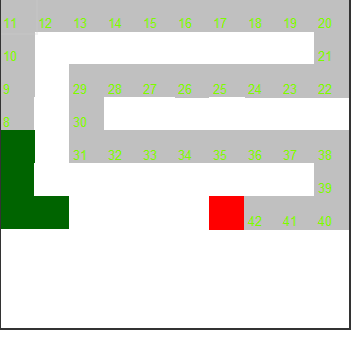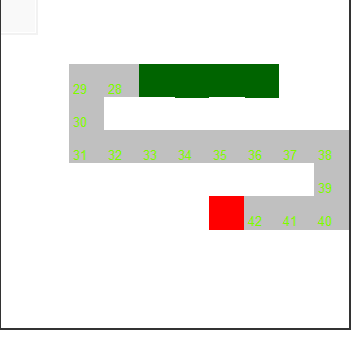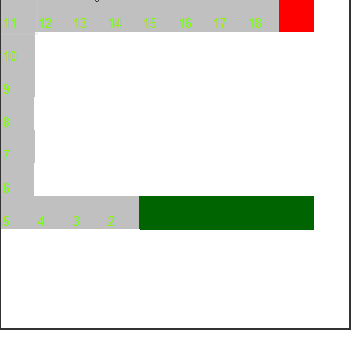
Алгоритм отлично работает до тех пор пока "хвост" змеи не начинает перекрывать кратчайший путь.
Серым цветом выделен рассчитанный путь.

Графики
2. Поиск в глубину (Depth-first search) Вики
Другой способ обхода графа, который ,как правило, будет приводить к более запутанному и сложному пути.
Поиск в глубину отличается тем, что сначала рассматриваются максимально далекие подчиненные текущего узла.
Отличие алгоритма от поиска в ширину будет минимальным: на шаге 2 берем узел не с вершины, а со дна стека.
Графики
3. Длиннейший путь
Если наша цель максимизировать количество очков, то можно удлинить путь к еде включая в него максимальное число соседних узлов.
Для этого получим кратчайший путь (поиском в ширину) и будем рассматривать каждые 2 узла пути. Если есть возможность, то включаем в путь 2 соседних.Повторяем упражнение пока расширение возможно.
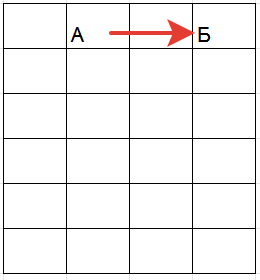
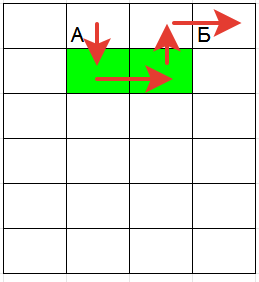

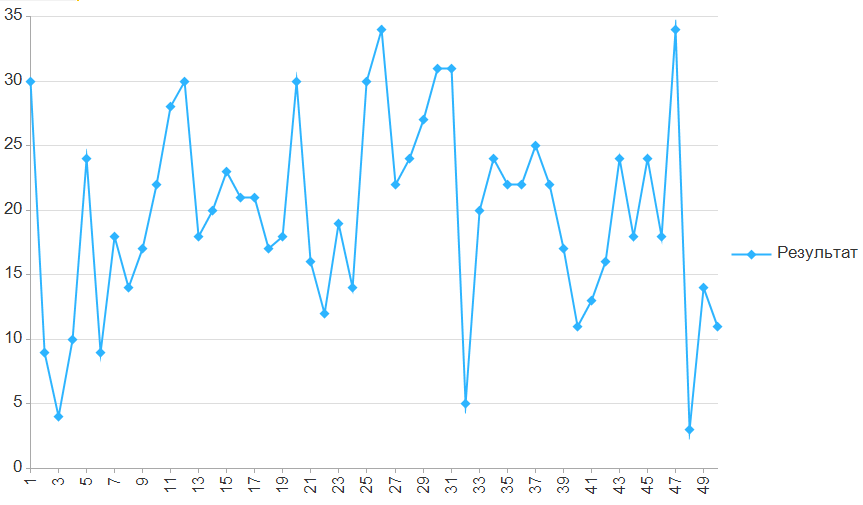
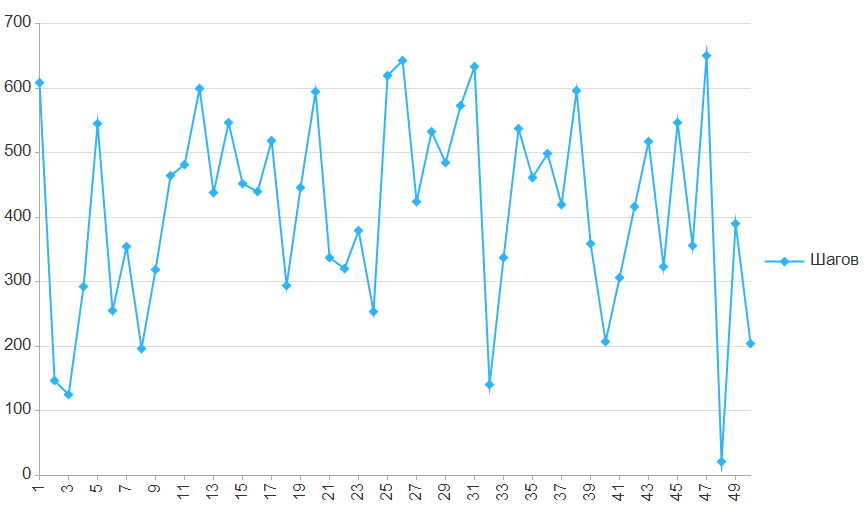
Графики
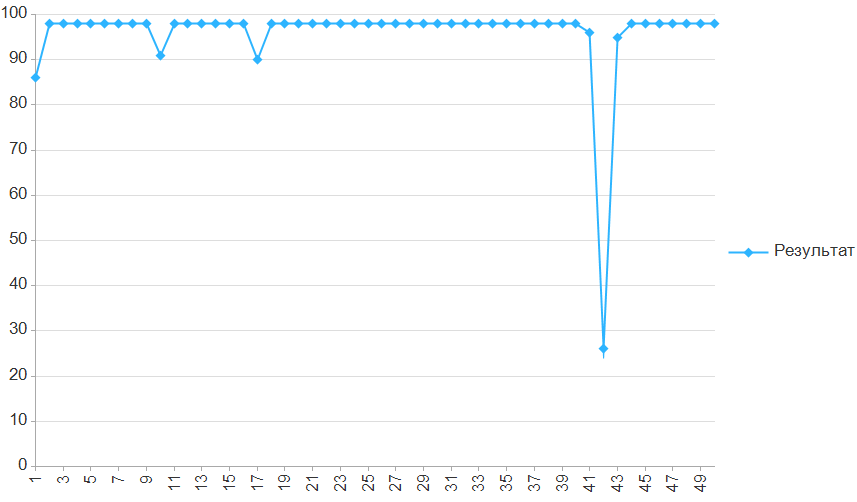
Результат увеличился, тем не менее, хвост все еще продолжает мешать.
4. Гамильтонов цикл Вики
Гамильтонов цикл — замкнутый цикл, который проходит через каждую вершину графа по одному разу.
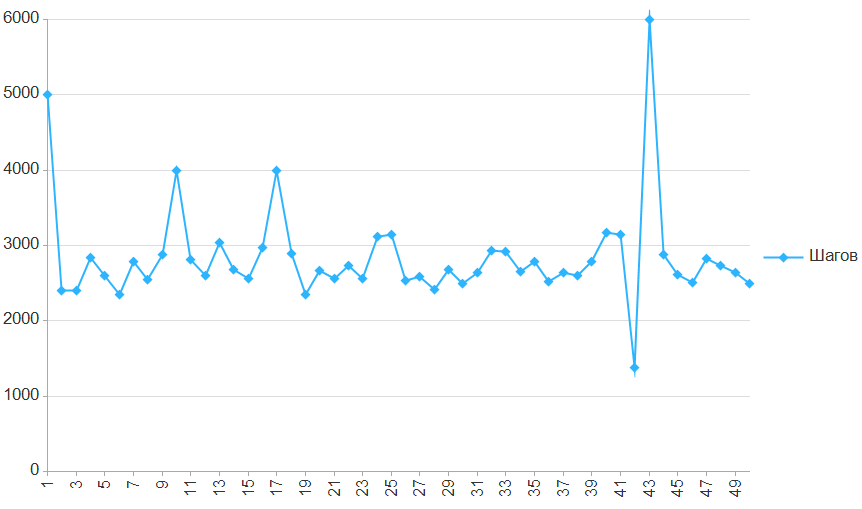
Если нас не волнует количество шагов, то можно посчитать длиннейший путь не к еде, а к хвосту. Т.к. длиннейший путь проходит по большинству ячеек поля, то еда будет съедена по пути, не зависимо от ее расположения.
В зависимости от расположения змеи могут образовываться недостижимые ячейки, поэтому, строго говоря, данный алгоритм не соответствует определению Гамильтонова цикла.

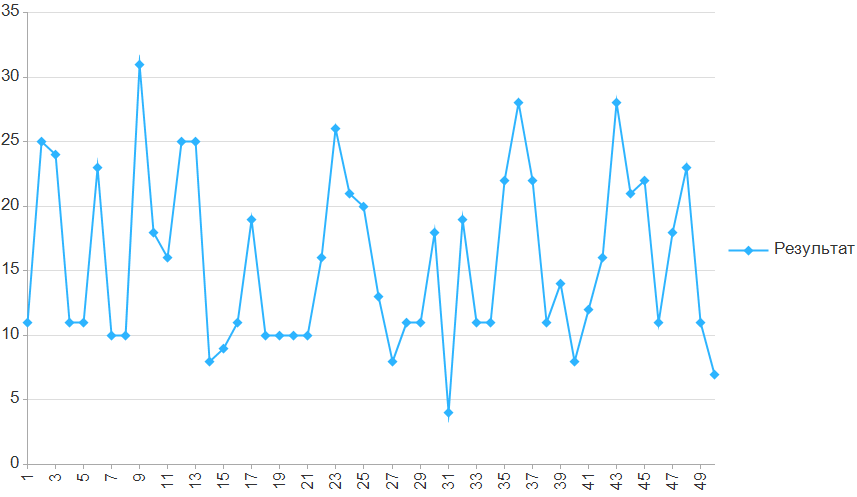
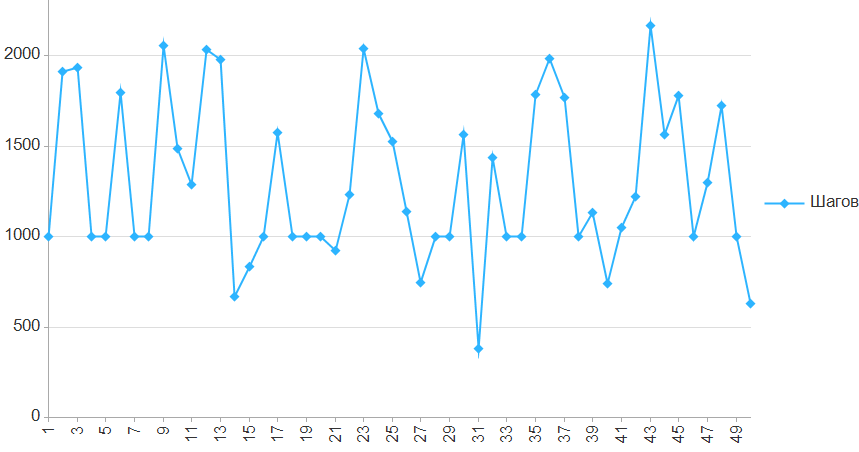
Графики
5. Гамильтонов цикл 2
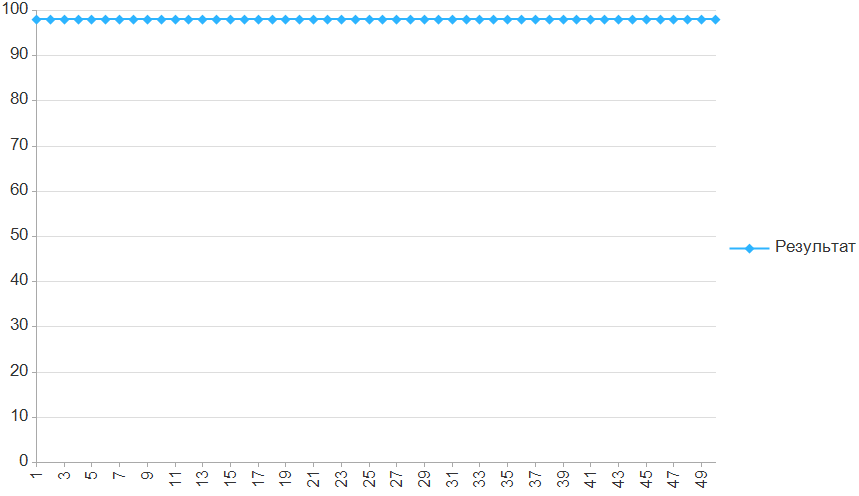
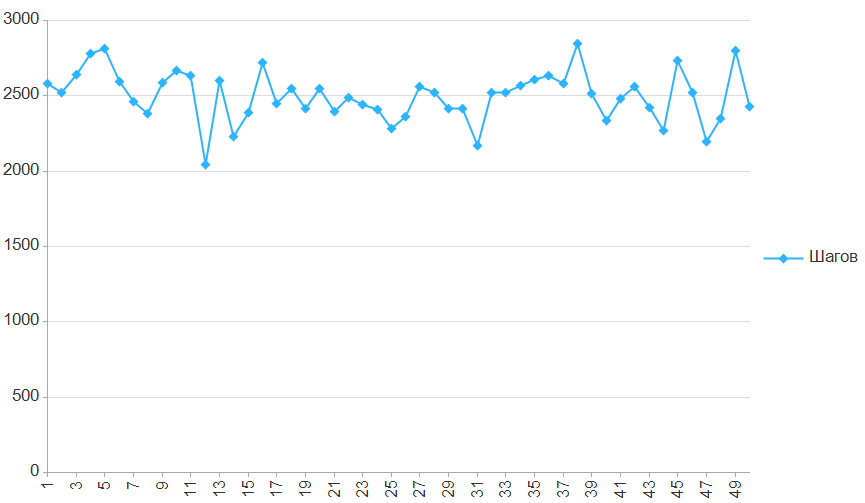
Самый простой алгоритм из описанных, обладает 100% эффективностью и не требует никаких расчетов.
Подойдет для любого прямоугольного поля на котором нет препятствий.
Если нас действительно не волнует число шагов, то можно просто ходить по зацикленному пути:
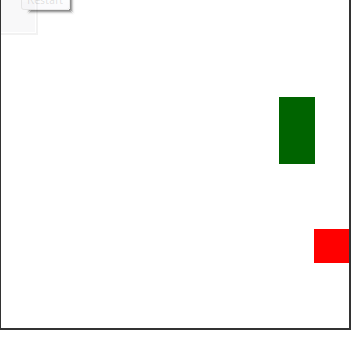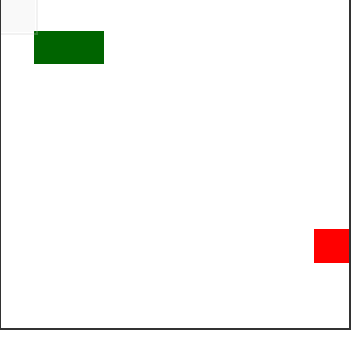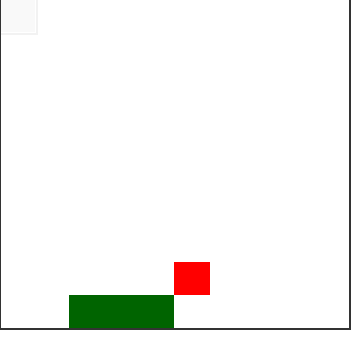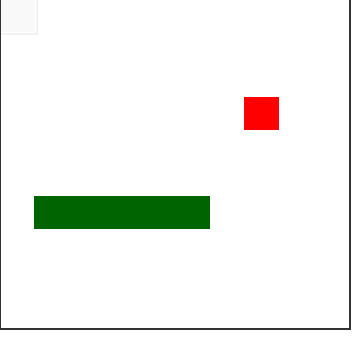
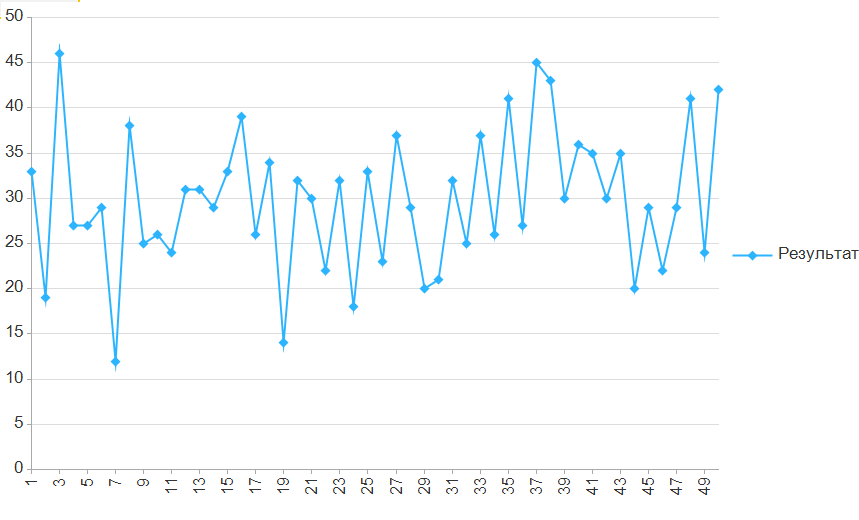
Графики
Обработка протестирована на 8.3.12.1595, 8.3.12.1855


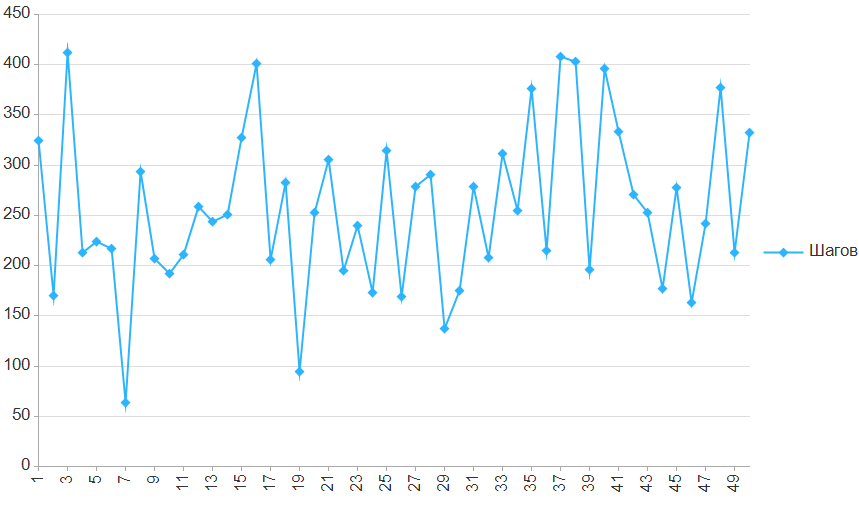




Ок, но при чем тут Искусственный интеллект — просто для словца?
Сначала такие проги писали на Бейсик под синклеры, сейчас на 1С под РС.
Те же шары, только вид сбоку
Мде, подвела ассоциативная цепочка «искусственный интеллект» -> «нейронные сети» и я пришел читать статью
А тут привет из 90-х, когда компьютеры были квадратными и оперативка измерялась килобайтами