В данной части статьи мы обсудим, каким образом в модели для расчета себестоимости появляются встречные затраты, называемые также затратами встречного выпуска или затратами на оказание встречных услуг. Надо отметить, что на данный момент нет какого-то общепризнанного строгого определения встречных затрат. Обычно, когда бухгалтеры и экономисты говорят о встречных затратах, то имеются в виду затраты, которыми подразделения предприятия обмениваются «одновременно», т.е. как бы в один и тот же момент времени. Эта тема уже обсуждалась в статье Как появляются встречные затраты, но, как оказалось, у многих читателей остались вопросы, поэтому в данной статье мы еще раз к ней вернемся.
Как уже должно быть понятно внимательному читателю из предыдущих частей статьи, сама по себе задача расчета стоимости встречных затрат не является проблемой для модели в виде Графа затрат. Более того, этот расчет вообще не имеет никакого смысла выделять в какую-то самостоятельную задачу и рассматривать его отдельно от общей процедуры расчета себестоимости, т.к. в результате решения СЛАУ определяются сразу все стоимости вторичных затрат – как встречных, так и «не встречных». Процедура решения СЛАУ при расчете себестоимости никак не меняется от того, есть ли в Графе затрат потоки встречных затрат или нет, поэтому саму технику расчета себестоимости с помощью СЛАУ обсуждать мы не будем, она точно такая же, как и в предыдущих частях статьи.
Какие же вопросы тогда имеет смысл обсудить по данной теме? В первую очередь это вопросы интерпретации полученных при решении СЛАУ стоимостей встречных затрат, поскольку учетные специалисты не всегда могут «грамотно» объяснить полученные результаты ни с математической, ни с экономической точки зрения. Также приходится признать, что у некоторых учетных специалистов могут возникать и определенные сложности психологического характера, когда, исходя из своего субъективного понимания хозяйственной ситуации, они просто не хотят «верить» в существование встречных затрат и рассматривают их как некое досадное недоразумение, от которого надо любым образом избавиться. Поэтому в данной статье на простейших моделях будут рассмотрены математические и экономические особенности расчета стоимости встречных затрат и будет показано (и даже доказано), что:
– причиной появления встречных затрат в модели для расчета себестоимости является применение взвешенной оценки стоимости активов предприятия – когда себестоимость материалов, продукции и т.п. рассчитывается только один раз в конце периода, например, при проведении процедуры «закрытия» затрат периода
– а в основе психологического неприятия некоторыми специалистами встречных затрат лежит всего лишь своего рода «конфликт интересов» – когда специалист на самом деле хочет видеть результаты расчета себестоимости на основе скользящей оценки, при которой стоимость каждой хозяйственной операции рассчитывается непосредственно в момент ее отражения в системе бухгалтерского учета, но(!) использует для этого модель на основе взвешенной оценки, когда расчет себестоимости производится только один раз в конце периода. В результате, ожидания пользователя не всегда оправдываются, он получает не всегда понятные ему результаты, в том числе и в виде появления встречных затрат. Вот, собственно, и вся «проблема»
Для понимания приведенных выше тезисов сравним между собой два способа оценки себестоимости – взвешенную (за период) и скользящую.
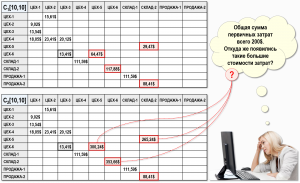
Рассмотрим простейшую хозяйственную ситуацию, связанную с перемещением материалов между двумя складами предприятия – на Склад-1 поступили материалы одной и той же номенклатуры, но приобретенные предприятием у двух поставщиков по разным ценам. От Поставщика-1 поступило 10кг материалов общей стоимостью 10$ (по цене 1$/кг), а от Поставщика-2 поступило 6кг материалов общей стоимостью 10$ (по цене 1,67$/кг). В течение рассматриваемого периода 5кг материалов со Склада-1 было перемещено на Склад-2, но затем, в этом же периоде, эти материалы были возвращены на Склад-1. В конце периода все 16кг материалов были перемещены со Склада-1 на Склад-2.
При отражении в системе бухгалтерского учета операций по списанию материалов со складов предприятия будем использовать оценку по средней себестоимости, но рассмотрим и сравним между собой два варианта ее применения:
Вариант 1 – скользящая средняя оценка, при которой фактическая себестоимость материалов определяется непосредственно в момент их отпуска со склада
Вариант 2 – взвешенная средняя оценка, при которой фактическая себестоимость ушедших со склада материалов определяется только в конце периода исходя из средней за период фактической себестоимости, в расчет которой включаются количество и стоимость материалов на начало периода и все поступления за период
Вариант 1. Скользящая средняя оценка стоимости материалов
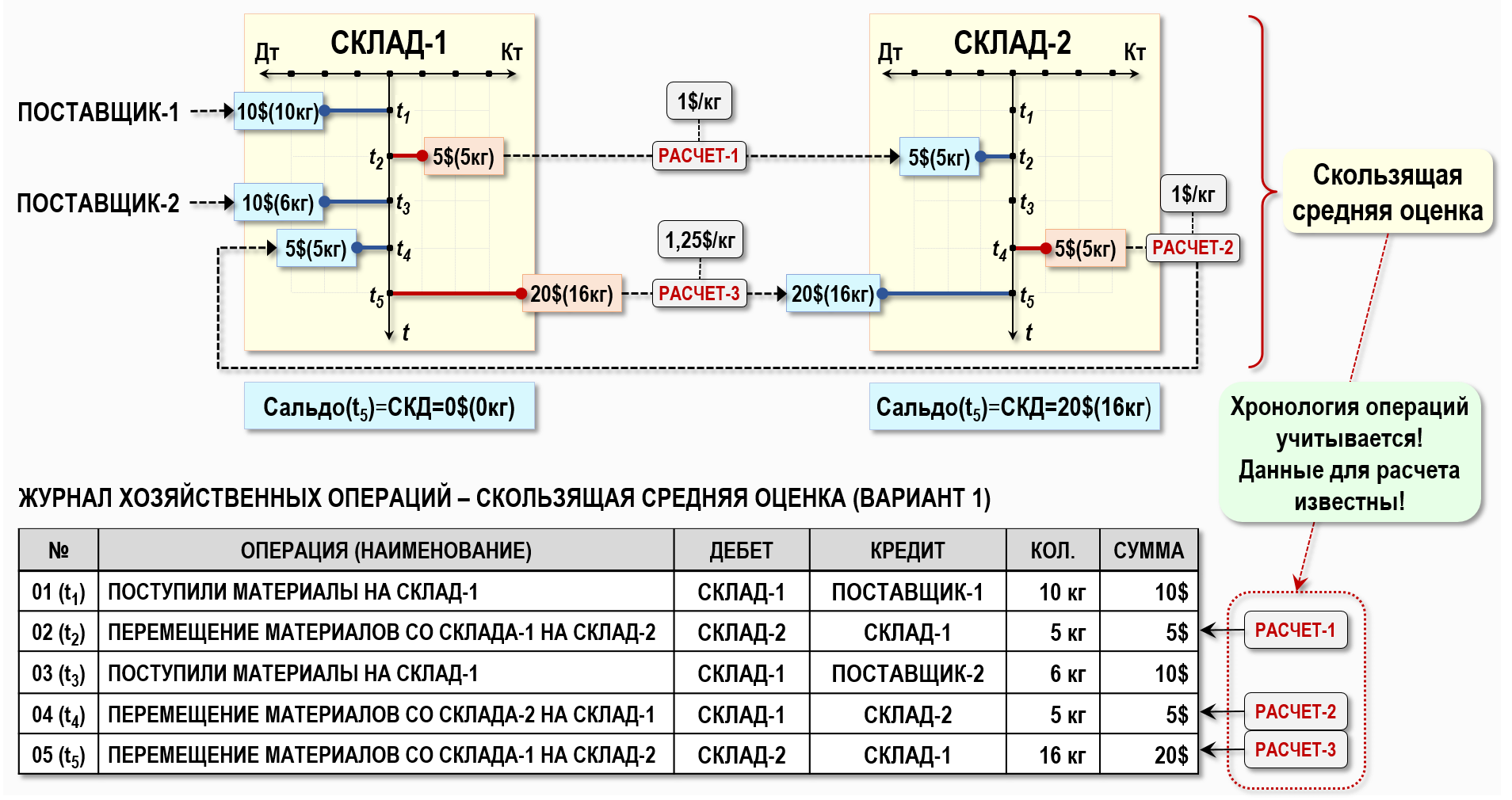
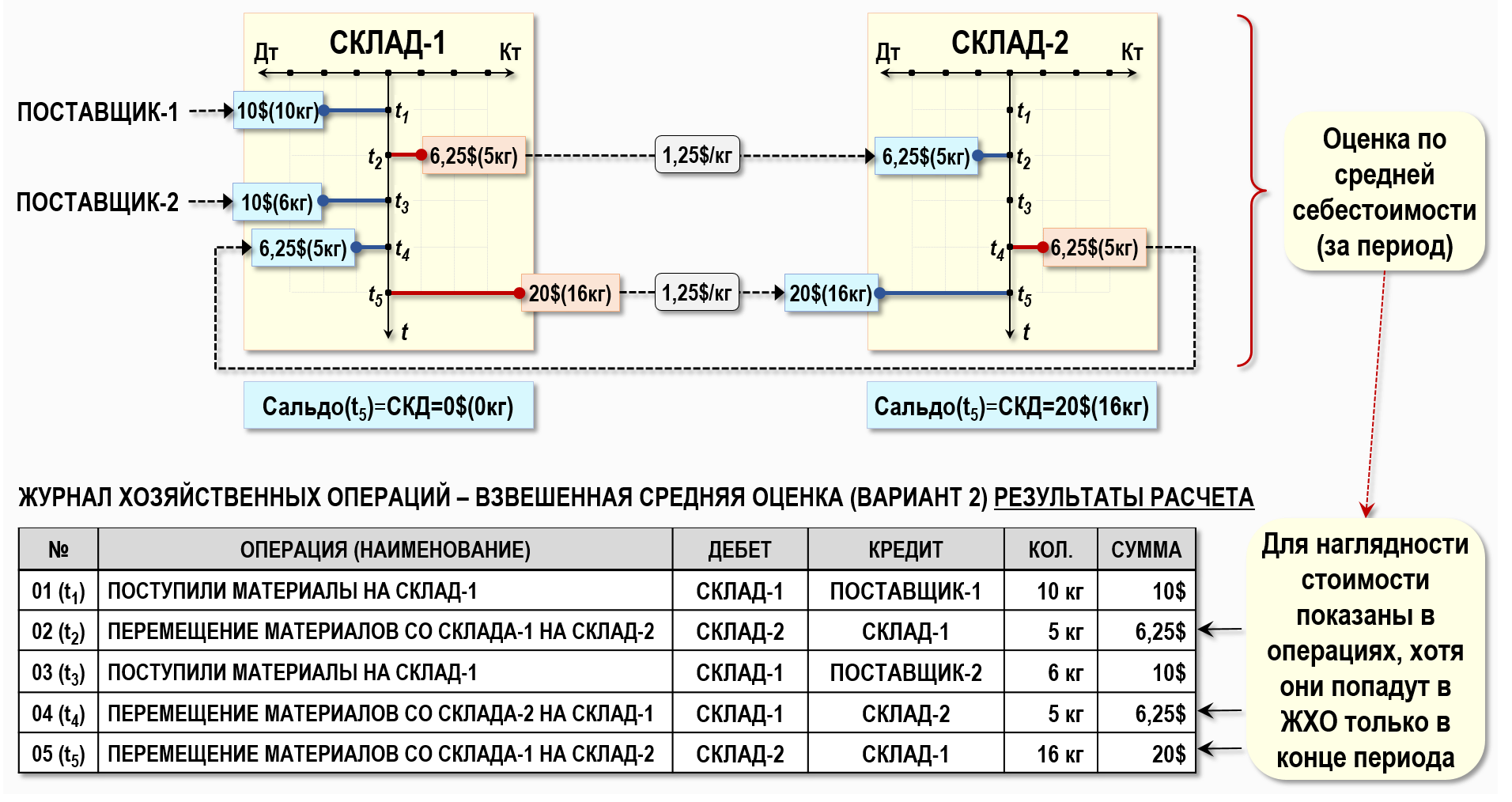
Представим рассматриваемую хозяйственную ситуацию на рисунке с помощью «самолетиков» и записей в журнале хозяйственных операций (ЖХО):
Рассматриваемая хозяйственная ситуация достаточно наглядно представлена выше на рисунке, тем более, что «самолетики» счетов учета изображены на нем в более строгом математическом виде, чем обычно это делают бухгалтеры. В данном случае «самолетик» изображен в виде системы координат, состоящей из оси времени и оси стоимости по дебету и по кредиту, что подчеркивает смысл использования данного абстрактного объекта для объяснения работы счета учета.
Основной смысл использования любой скользящей оценки, в том числе и скользящей средней оценки, состоит в том, что фактическая себестоимость материалов рассчитывается непосредственно в тот момент времени, когда в ЖХО отражается операция по списанию материалов со склада предприятия. В нашем примере таких операции три – 02(t2), 04(t4) и 05(t5), а значит расчет фактической себестоимости материалов при использовании скользящей оценки должен происходить непосредственно в моменты времени t2, t4 и t5:
Расчет-1 (t2): со Склада-1 списано 5кг материалов общей стоимостью 5$, себестоимость 1кг материала составила 1$
Расчет-2 (t4): со Склада-2 списано 5кг материалов общей стоимостью 5$, себестоимость 1кг материала составила 1$
Расчет-3 (t5): со Склада-1 списано 16кг материалов общей стоимостью 20$, себестоимость 1кг материала составила 1,25$
Сами по себе расчеты вполне очевидны, поэтому здесь не приводятся, читатель легко их может провести самостоятельно. Для целей настоящей статьи нас в первую очередь интересует тот факт, что эти три расчета себестоимости списанных со складов материалов можно провести непосредственно(!) в указанные моменты времени. Действительно, для проведения каждого из трех расчетов в соответствующий момент времени у нас есть все необходимые для этого данные – количества и стоимости материалов, накопленных к каждому моменту времени по дебету счетов учета Склад-1 и Склад-2. Именно поэтому существует возможность определения стоимостей операций в хронологической последовательности их появления в ЖХО. Но если бухгалтер примет решение использовать взвешенную среднюю оценку стоимости материалов, то ситуация кардинально изменится.
Вариант 2. Взвешенная средняя оценка стоимости материалов
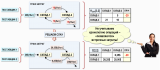
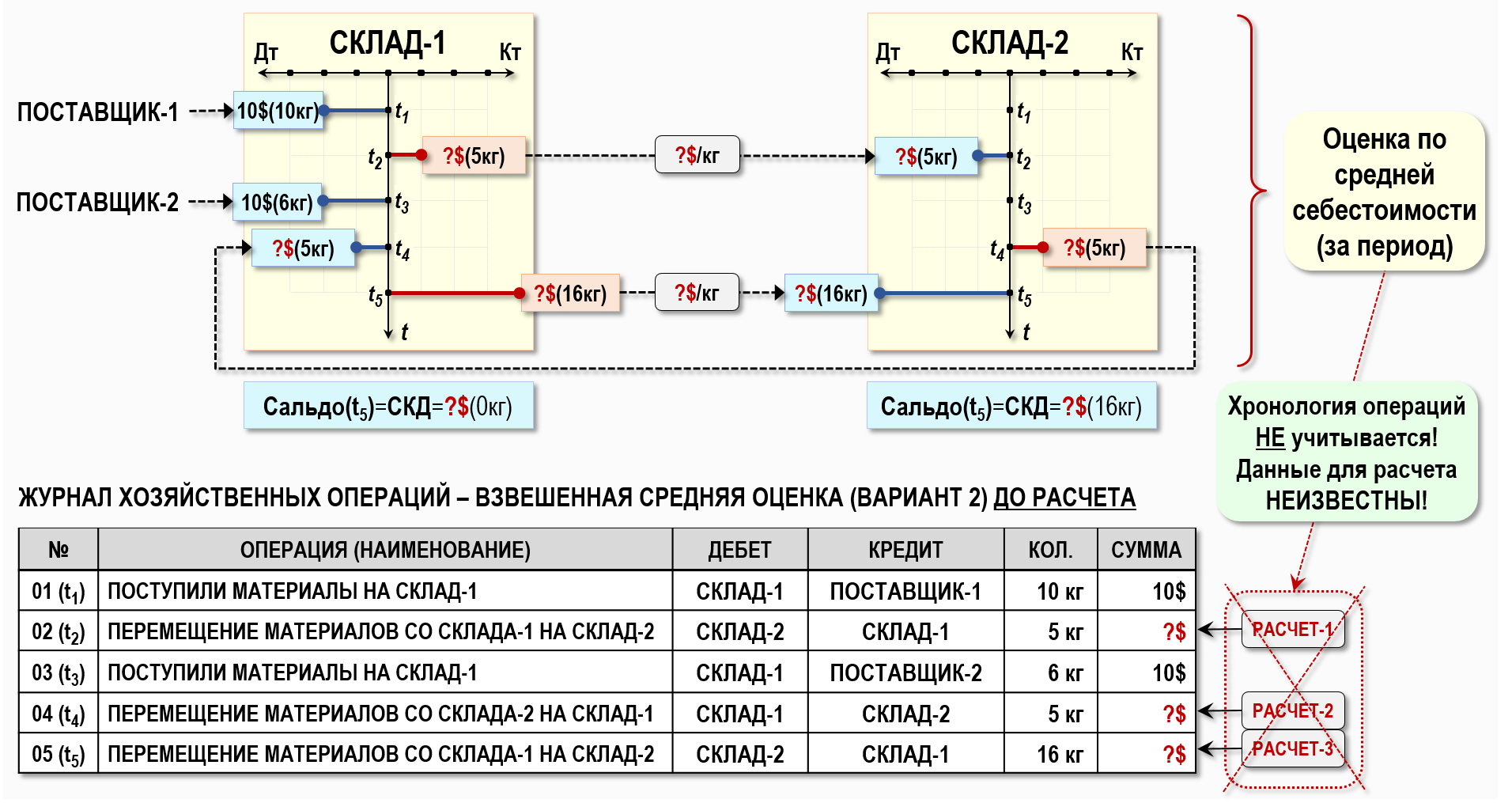
Представим рассматриваемую хозяйственную ситуацию на рисунке с помощью «самолетиков» и записей в ЖХО:
Как видим, ситуация кардинально изменилась – теперь уже не получится рассчитать себестоимость списанных со складов материалов непосредственно в моменты времени t2, t4 и t5, как при скользящей оценке. Это связано с тем, что использование взвешенной средней оценки предполагает проведение расчета фактической себестоимости материалов только один раз в конце периода [t1,t5]. Как провести расчет себестоимости для данного варианта? Думаю, внимательные читатели уже догадались – для этого надо воспользоваться моделью в виде Графа затрат.
Мы уже умеем решать СЛАУ для Графов затрат, поэтому не будем рассматривать это решение подробно, но только отметим две особенности для данного случая.
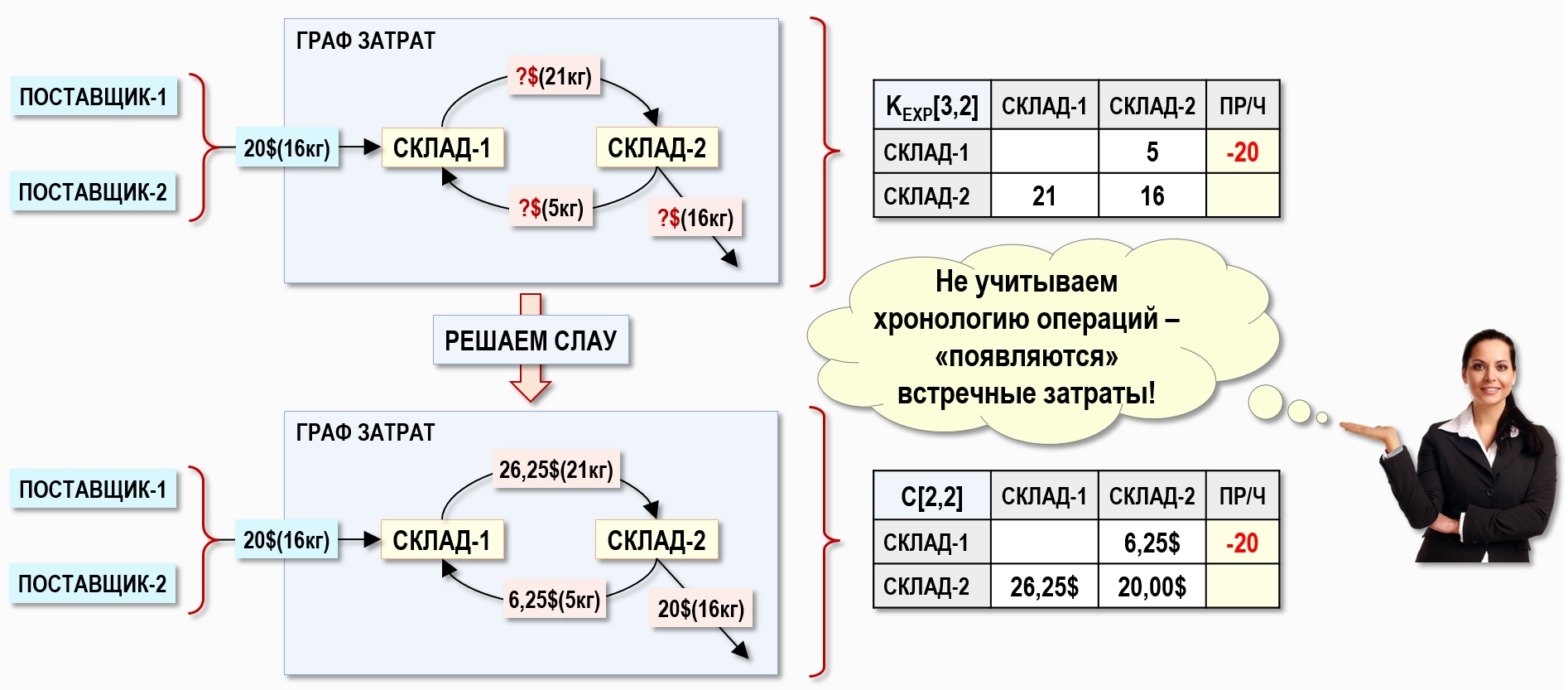
Во-первых, на главной диагонали расширенной матрицы исходных коэффициентов KEXP[3,2] на пересечении столбца и строки для Склада-2 появляется значение 16кг, которое соответствует количеству материалов, оставшихся на Складе-2 на конец периода, т.е. в этой ячейке отражено «количественное» сальдо по дебету счета Склад-2 на конец периода. Подробнее о данной особенности можно посмотреть в статье Когда неизвестны затраты в НЗП на конец периода (продукция на складе). Все остальные этапы решения СЛАУ остаются такими же, как и раньше.
Во-вторых, узел Склад-2 имеет на рисунке исходящую дугу, которая не соединяет его с каким-либо другим узлом Графа затрат – это способ графического изображения остатка материалов на Складе-2 на конец периода. Если бы на Складе-2 имелся остаток материалов на начало периода, то эту ситуацию мы бы изобразили входящей дугой, начало которой не было бы связано ни с каким другим узлом Графа затрат.
Как видим выше на рисунке, между складами появились встречные затраты. Это произошло потому, что при использовании взвешенной средней оценки себестоимости хронология операций в ЖХО игнорируется, и все операции внутри периода [t1,t5] рассматриваются так, как будто бы они были отражены в ЖХО одномоментно. Другими словами, удалив из модели для расчета себестоимости фактор времени, пользователь лишается возможности «заглянуть» внутрь того периода, для которого рассчитывается себестоимость, он уже не может различить операции по времени их появления в ЖХО и рассчитать их стоимость с помощью скользящей средней оценки. Расчет стоимости происходит только один раз сразу для всех операций за период («оптом») и в результате, даже если реальные взаимные перемещения материалов между складами происходили в разные моменты времени внутри рассматриваемого периода, то в модели для расчета себестоимости они будут рассматриваться так, как будто эти перемещения происходили одномоментно, т.е. будут отражаться в виде встречных затрат. В этом случае для расчета себестоимости материалов имеет значение только общее за период количество перемещенных между складами материалов, что и нашло свое выражение в расширенной матрице исходных коэффициентов KEXP[3,2] и матрице стоимостей C[2,2]:
– на Склад-1 со Склада-2 поступило за период 5кг материалов общей стоимостью 6,25$
– на Склад-2 со Склада-1 поступило за период 21кг материалов общей стоимостью 26,25$, ушло со Склада-2 5кг материалов стоимостью 6,25$, осталось в конце периода на Складе-2 16кг материалов стоимостью 20$
В данном случае поступившие на Склад-1 от поставщиков 16кг материалов стоимостью 20$ рассматриваются как первичные затраты, стоимость которых заранее известна. С помощью решения СЛАУ эту стоимость определять не нужно, она формирует правую часть уравнения баланса затрат для Склада-1 за рассматриваемый период. Для целей расчета себестоимости с помощью СЛАУ количество первичных затрат значения не имеет, важно только количество материалов, перемещенных между складами, ведь именно их стоимость определяется в результате решения СЛАУ.
Особо стоит обратить внимание на общее количество (21кг) и стоимость материалов (26,25$), ушедших со Склада-1 на Склад-2. По условиям задачи от обоих поставщиков на Склад-1 поступило в общей сложности только 16кг материалов стоимостью 20$. Далее эти материалы только перемещались между складами, откуда же взялось такое большое количество и стоимость материалов? Это и есть особенность математической модели для расчета себестоимости с помощью взвешенной средней оценки. Поскольку в этом случае модель не учитывает хронологическую последовательность перемещения материалов, то получается, что внутри периода многократные перемещения материалов со Склада-1 на Склад-2 складываются между собой и для расчета себестоимости считаются одним «общим» перемещением материалов (21кг) стоимостью 26,25$.
Это важная особенность данной модели, ее следствием является то, что в этом случае стоимость вторичных затрат рассматривается как сугубо расчетная(!) величина, которая просто помогает определить сальдо счетов учета на конец периода, но сама по себе не всегда соответствует «реальной» стоимости перемещаемых ресурсов предприятия.
Представим результаты расчета при использовании взвешенной средней оценки себестоимости с помощью «самолетиков» и записей в ЖХО:
Для наглядности все стоимости материалов на рисунке показаны в «своих» операциях, хотя фактически эти стоимости попадут в ЖХО только после проведения процедуры «закрытия» затрат периода и будут отражены с помощью дополнительных записей в ЖХО в конце периода.
На рисунке видно, что сумма хозяйственной операции 02(t2) составляет 6,25$ за 5кг материала, т.е. себестоимость 1кг равна 1,25$/кг, хотя на самом деле, если провести расчет себестоимости с помощью скользящей оценки, то на момент времени t2 на Складе-1 имеется только 10кг материала стоимостью 10$, а значит – себестоимость 1кг должна составлять 1$/кг. Это своего рода «расплата» за использование более упрощенной модели для расчета себестоимости, основанной на использовании взвешенной средней оценки стоимости материалов. Действительно, такая модель предполагает проведение всего одного расчета себестоимости в конце периода вместо многократных расчетов в случае использования скользящей средней оценки стоимости материалов – и за эту «простоту» приходится расплачиваться не всегда понятными результатами расчета.
Здесь имеет смысл сказать, что изменение правил бухгалтерского учета не всегда успевает за изменениями в реальной экономической жизни – и применение взвешенной оценки стоимости это хорошо иллюстрирует. Например, в РАУЗ 1С есть такая опция – возможность оценивать стоимость МПЗ и затрат по плановым или другим ценам в течение периода, не дожидаясь расчета себестоимости в конце периода. Появление этой опции объясняют тем, что пользователи хотят иметь хоть какое-то представление о стоимости МПЗ и затрат в момент отражения операций в системе учета. И надо признать, что в современных условиях интенсификации производства и волатильности рынка это желание абсолютно логично, а иногда и критически важно для ведения бизнеса. На языке математики это желание пользователей можно сформулировать следующим образом – на самом деле пользователи предпочли бы использовать скользящую оценку стоимости, а не взвешенную по окончании периода. Фактически это означает, что пользователи хотели бы использовать для расчета себестоимости другую (скользящую) математическую модель, но им предлагают использовать все ту же модель (взвешенную), только слегка подкорректированную. И хотя действующими бухгалтерскими правилами разрешено использование как взвешенной, так и скользящей оценок стоимости, в современных условиях бурного развития информационных технологий пользователи систем учета все-таки рассчитывают на более оперативное получение учетных данных, что возможно только в случае использования скользящих оценок стоимости.
Таким образом, в результате анализа простейшей хозяйственной операции по перемещению материалов между двумя складами мы выяснили, что появление встречных затрат в модели для расчета себестоимости является прямым следствием использования взвешенной средней оценки стоимости, при которой фактическая себестоимость материалов рассчитывается только один раз в конце периода. Это особенность данной модели, которую пользователи должны учитывать в своей работе.
Также надо понимать, что, хотя математические модели для расчета стоимости материалов, использующие взвешенную среднюю оценку и скользящую среднюю оценку существенно различаются между собой, обе модели корректны и адекватно описывают соответствующие бухгалтерские правила оценки стоимости материалов при их списании со складов предприятия. Просто надо учитывать последствия выбора первого или второго варианта модели прежде, чем зафиксировать этот выбор в положении об учетной политике предприятия, чтобы у пользователя потом не возникло «конфликта интересов», о котором говорилось в начале статьи.
Обсуждение вопроса о встречных затратах в статье специально было начато с рассмотрения простейшей ситуации перемещения материалов между складами предприятия, чтобы читатель убедился в том, что встречные затраты могут появиться в любом месте модели предприятия. Причиной появления встречных затрат в модели для расчета себестоимости является использование взвешенной оценки стоимости, а избежать появления встречных затрат можно только в случае использования скользящих оценок стоимости, когда стоимость каждой операции рассчитывается непосредственно в момент ее отражения в ЖХО.
Модель в виде Графа затрат также позволяет дать строгое определение встречных затрат – если два узла Графа затрат достижимы друг из друга, то эти два узла связаны между собой встречными затратами. Другими словами, если для пары узлов существуют потоки затрат из первого узла во второй, а также потоки затрат – из второго узла в первый, то между этими узлами существуют встречные затраты. В этом случае говорят, что оба узла находятся в одном контуре, т.к. из любого узла в этом контуре можно пройти по потокам затрат контура и вернуться обратно в этот же узел.
Кстати, рассмотренный нами пример наглядно показывает, в чем состоит проблема использования в подсистеме РАУЗ 1С взвешенной оценки по ФИФО. Основная концепция РАУЗ состоит в едином подходе к расчету стоимости МПЗ и затрат. Но дело в том, что в этом случае суммы всех операций по перемещению МПЗ между складами рассчитываются только один раз в конце периода с помощью решения СЛАУ, т.е. с помощью взвешенной средней оценки. Поэтому либо надо запрещать пользователям отражать в системе учета любые перемещения между складами, либо отказываться от взвешенной оценки по ФИФО и использовать только взвешенную среднюю оценку стоимости, либо отказываться от этой весьма спорной концепции. Подробнее этот вопрос рассмотрен в статье ФИФО (РАУЗ) – работает или не работает? Почему концепция объединения в «одном флаконе» МПЗ и затрат является спорной? Потому, что в современных условиях наиболее предпочтительным для пользователей систем учета все-таки является применение скользящей оценки стоимости (средней, ФИФО), позволяющей рассчитывать стоимости хозяйственных операций оперативно – непосредственно в момент их отражения в системе учета. Иногда скользящий способ оценки стоимости ошибочно называют партионным учетом, но партионный учет предполагает, что единицей учета является партия материалов, товаров и т.д., а «обычный» учет МПЗ (не РАУЗ) — производится с помощью скользящей оценки стоимости. Таким образом, не очень понятно, зачем уходить от скользящей оценки стоимости МПЗ и заменять ее на взвешенную (в РАУЗ), упрощая и даже огрубляя тем самым модель для расчета стоимости МПЗ. Если для расчета стоимости затрат применение скользящей оценки стоимости пока еще действительно является проблемой, то для расчета стоимости МПЗ никаких особых проблем с применением скользящих оценок не возникает.
Несколько «полезных» комментариев:
Не является секретом, что среди специалистов-практиков (бухгалтеров, экономистов, программистов) пользуется определенной популярностью точка зрения, в соответствии с которой математические модели — это конечно хорошо и даже красиво, но(!) … ужасно оторвано от реальности. Ученые что-то там «напридумывали» для своего удовольствия, но мы-то (специалисты-практики) знаем, как все происходит на самом деле – «по-настоящему», а не на основе каких-то там моделей, тем более математических. В частности, именно таким образом воспринимаются некоторыми специалистами и модели в виде Графов затрат – как некая игра ума, не имеющая практического применения. К этой же категории непонятных и «ненужных» специалистам-практикам явлений относят и встречные затраты при расчете себестоимости.
Подобный сугубо практический подход к восприятию явлений реального мира, в том числе и к восприятию экономических явлений, давно известен науке, диагноз давно поставлен и называется – отождествление разных уровней абстракций. Проще говоря, специалист начинает безоговорочно отождествлять события реального мира со своими устойчивыми субъективными представлениями об этих событиях, не понимая, что имеет дело всего лишь с моделями этих событий. Например, как если бы путешественник стал считать, что карта местности – это и есть сама местность, при этом отрицал бы, что карта является абстрактной (математической) моделью, и был бы твердо убежден, что всякие ученые-картографы занимаются ерундой, не имеющей никакого практического применения, ведь путешественник лично ходит по реальным оврагам, болотам и т.п., а потому лучше знает, как все выглядит «по-настоящему». При этом, однако, путешественник с удовольствием пользуется GPS-навигатором с цифровыми картами, в основе работы которого лежат довольно серьезные математические модели, например, учитывающие релятивистские эффекты, описываемые общей теорией относительности. Хотя с точки зрения обычного путешественника – он просто ткнул пальцем в экран навигатора и проложил маршрут, и причем тут какая-то теория относительности?
У бухгалтеров это проявляется в том, что они считают, что система бухгалтерского учета имеет дело с «реальными» товарами, материалами, объектами основных средств и т.п., и никакие абстрактные модели не имеют к этому никакого отношения … ибо страшно далеки они от реальности. Причем бухгалтеру часто даже не приходит в голову, что все его представления о «реальных» объектах учета как раз и основаны исключительно на применении бухгалтерских абстракций – счетов учета и их корреспонденций, да еще на балансовых уравнениях для счетов учета. Все свои профессиональные знания бухгалтер изначально получает именно из абстрактных бухгалтерских моделей, но почему-то не хочет это признавать, считая, что получил знания об экономической реальности как-бы «напрямую», без помощи каких-то там моделей. Как следствие, в своей работе бухгалтер скорее готов ориентироваться на собственные, подчас откровенно интуитивные представления о хозяйственных процессах предприятия, чем опираться на понятные и строгие математические модели. Однако, как было показано выше, даже простейший анализ всем известных математических моделей в виде «самолетиков», используемых бухгалтерами для объяснения работы счетов бухгалтерского учета, опровергает эту весьма популярную точку зрения. Бухгалтер настолько привык пользоваться математическими моделями, что просто уже не осознает этого и более того, даже часто выступает против их использования в своей профессиональной деятельности. Подобные «кульбиты» мышления возникают просто от недостатка знаний как в своей предметной области, так и знаний общего характера, но эта ситуация поправима.
Напомним, что любая система бухгалтерского учета имеет дело исключительно с абстрактными объектами (моделями), т.е. с некими мысленными представлениями бухгалтера о реальных процессах хозяйственной деятельности предприятия, а автоматизированная система бухгалтерского учета представляет собой компьютерную модель реальных хозяйственных процессов, предназначенную для наблюдения за этими процессами. В основе любой компьютерной модели всегда лежит математическая, т.е. абстрактная модель предметной области, поэтому пользователь такой модели имеет дело не с объектами реального мира – материалами, товарами и т.д., а только с их абстрактными (математическими) моделями, причем «реальные» материалы и товары точно так же отражаются в системе бухгалтерского учета с помощью абстракций, как и такие невидимые и неосязаемые органами чувств бухгалтера объекты (иногда их называют виртуальными объектами учета), как расход, доход, прибыль и капитал.
Используя географическую аналогию можно сказать, что любая бухгалтерская модель представляет собой цифровую «карту» реальных хозяйственных процессов, аналогичную географической карте местности. Понятно, что географическую карту нельзя отождествлять с реальным рельефом местности, она является всего лишь математической моделью, которая с определенной степенью точности изображает местность с помощью условных знаков – сетки параллелей и меридианов, цветовых оттенков для обозначения высоты или глубины, различных числовых характеристик и т.д. Эти условные знаки (абстракции) не существуют в реальном мире, их нельзя увидеть на реальной местности, они являются только элементами модели. Бухгалтерская модель строится на аналогичных принципах – бухгалтерская цифровая «карта» реальных хозяйственных процессов формируется с помощью таких бухгалтерских абстракций, как счета учета, корреспонденции счетов учета, балансовые уравнения, а также с помощью различных бухгалтерских правил, регламентирующих использование счетов учета и их корреспонденций в различных ситуациях, в том числе и определяющих алгоритмы расчета сумм корреспонденций счетов учета. Так что без математических моделей в бухгалтерском учете обойтись невозможно.
И в заключительной части данной статьи рассмотрим некоторые интересные особенности поведения встречных затрат в математической модели для расчета себестоимости.
ЗАДАЧА 4. Расчет стоимости встречных затрат (большие стоимости)
Рассмотрим Граф затрат, известный нам из предыдущих частей статьи. Предприятие осуществляет два вида деятельности – производит и продает два вида продукции. В рассматриваемом периоде Цех-4 произвел и поместил на Склад-1 первый вид продукции в количестве 10 шт, а Цех-6 произвел и поместил на Склад-2 20 кг второго вида продукции. Со Склада-1 вся продукция была продана за 120$.
Далее рассмотрим два варианта сценария производственной программы:
Вариант 1 – 15 кг продукции со Склада-2 было продано, а 5 кг продукции со Склада-2 было использовано в этом же периоде Цехом-5
Вариант 2 – 5 кг продукции со Склада-2 было продано, а 15 кг продукции со Склада-2 было использовано в этом же периоде Цехом-5
В обоих вариантах было произведено и помещено на Склад-2 одно и то же количество продукции (20кг). Разница заключается только в количестве продукции, проданной со Склада-2 и использованной Цехом-5.
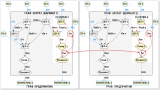
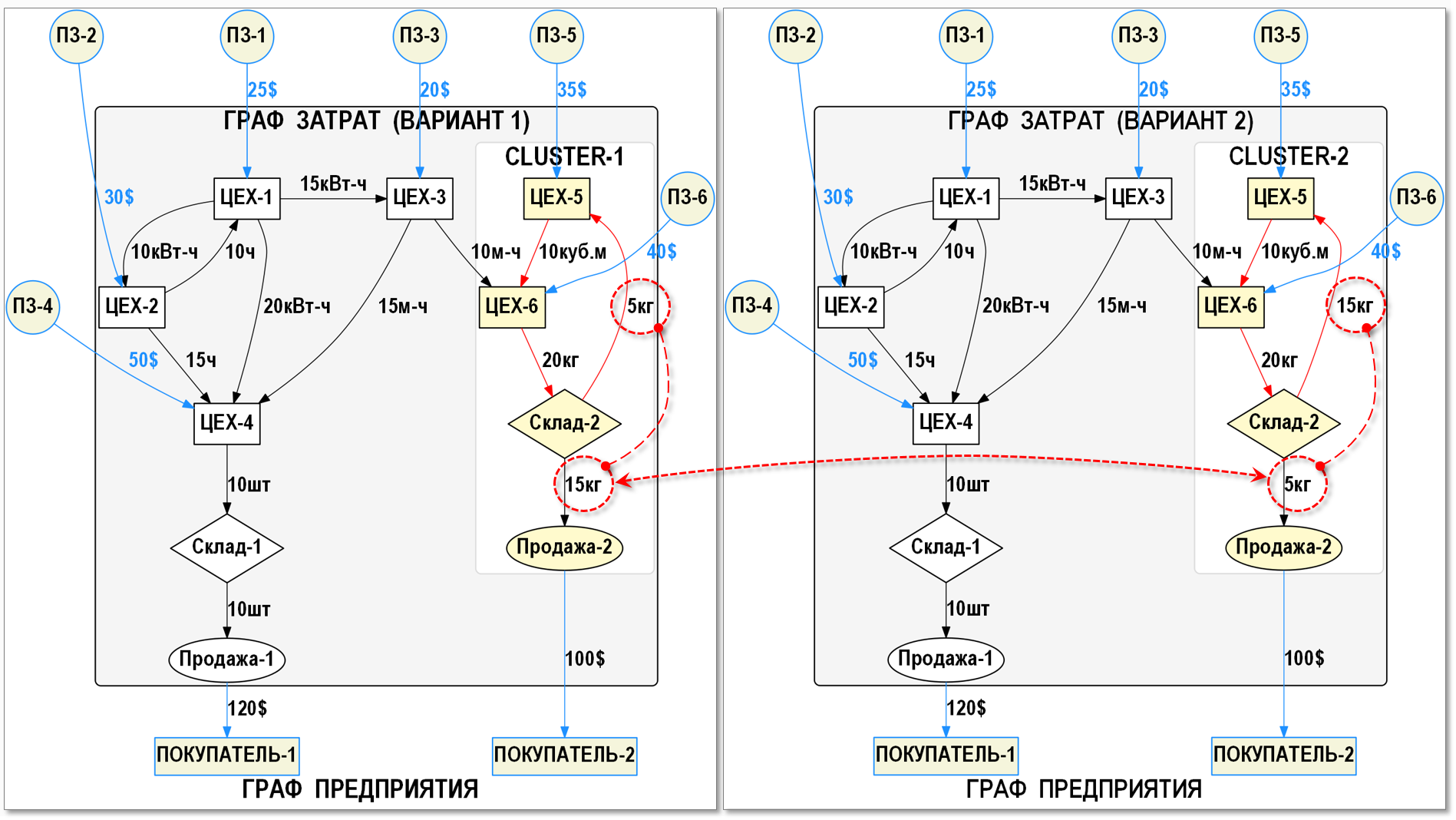
Мы не будем подробно описывать все хозяйственные операции предприятия, т.к. все они (до проведения процедуры «закрытия» затрат периода) для обоих вариантов представлены ниже на рисунке в графической форме, которая дает довольно ясное представление о том, как взаимодействуют между собой цеха предприятия при производстве обоих видов продукции.
На рисунке в обоих Графах затрат выделены фрагменты (кластеры), на которых хорошо видно, в чем заключается разница между двумя сценариями производственной программы предприятия:
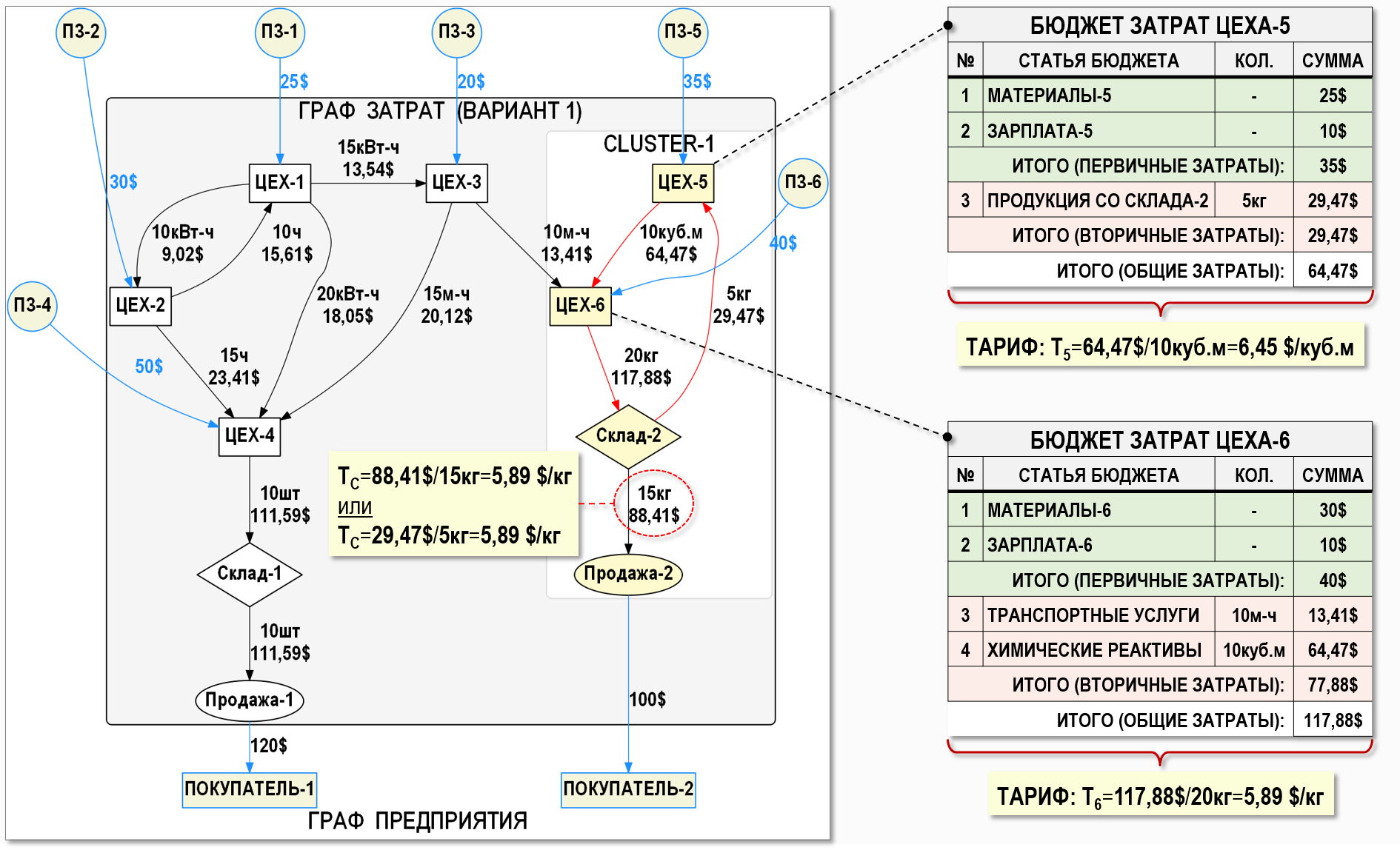
– в Cluster-1 на Склад-2 поступает 20кг продукции, а далее 15кг продается покупателям и 5кг поступает в Цех-5
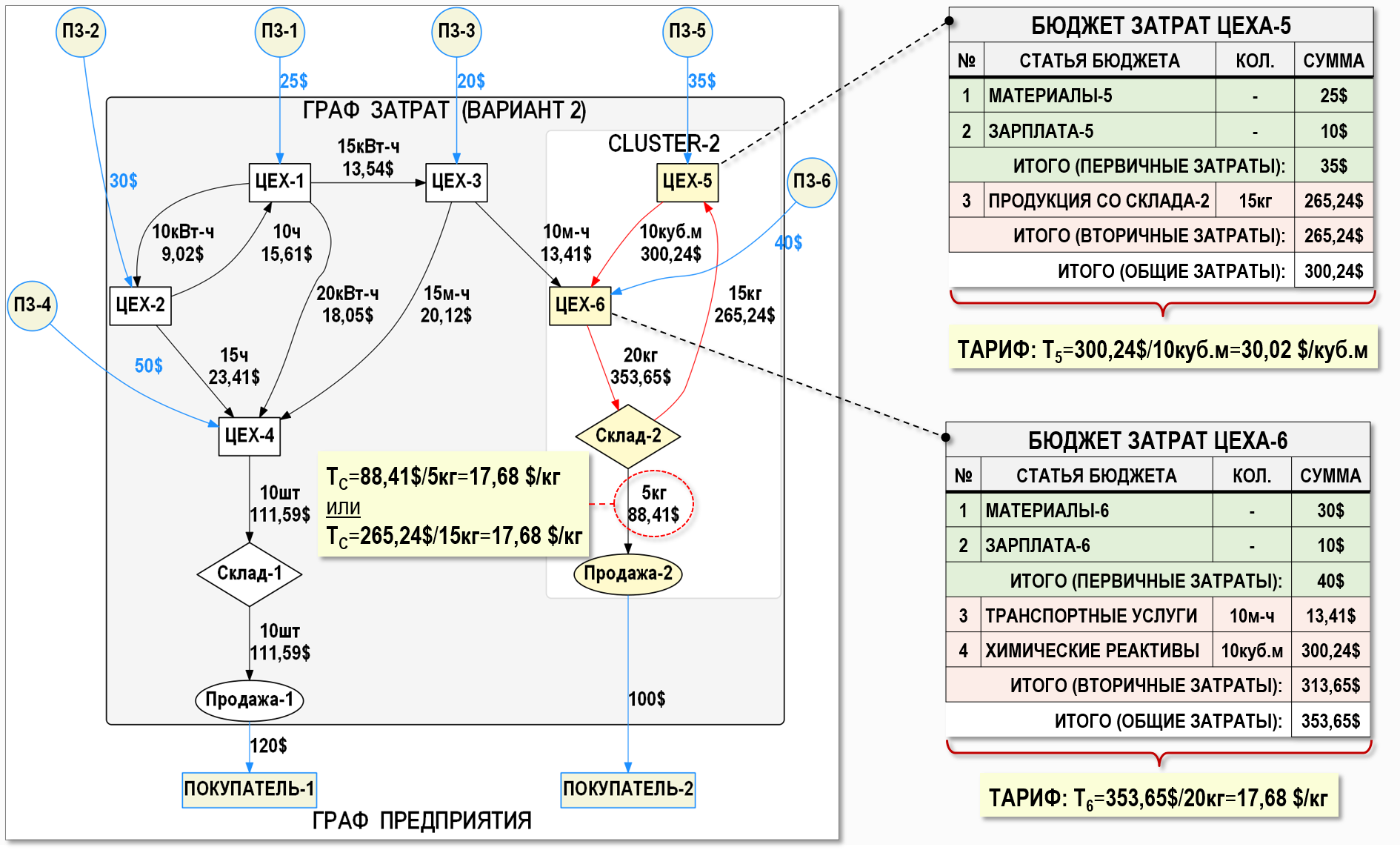
– в Cluster-2 на Склад-2 поступает также 20кг продукции, но продается покупателям только 5кг, а 15кг поступает в Цех-5
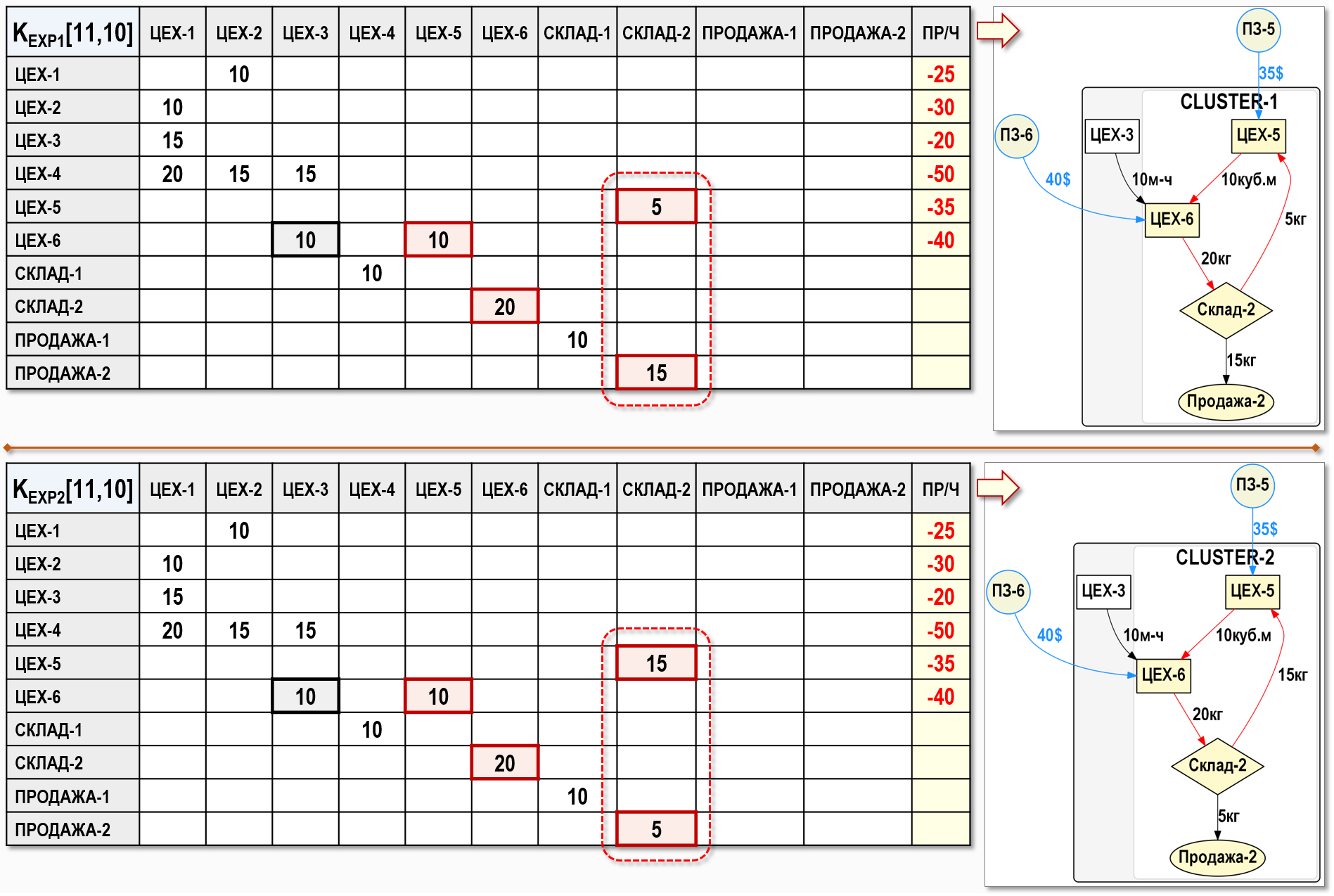
Составим расширенные матрицы исходных коэффициентов KEXP1[11,10] и KEXP2[11,10] для обоих вариантов:
Для наглядности рядом с матрицами исходных коэффициентов показаны фрагменты Графов затрат (кластеры) для соответствующих сценариев производственной программы.
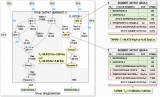
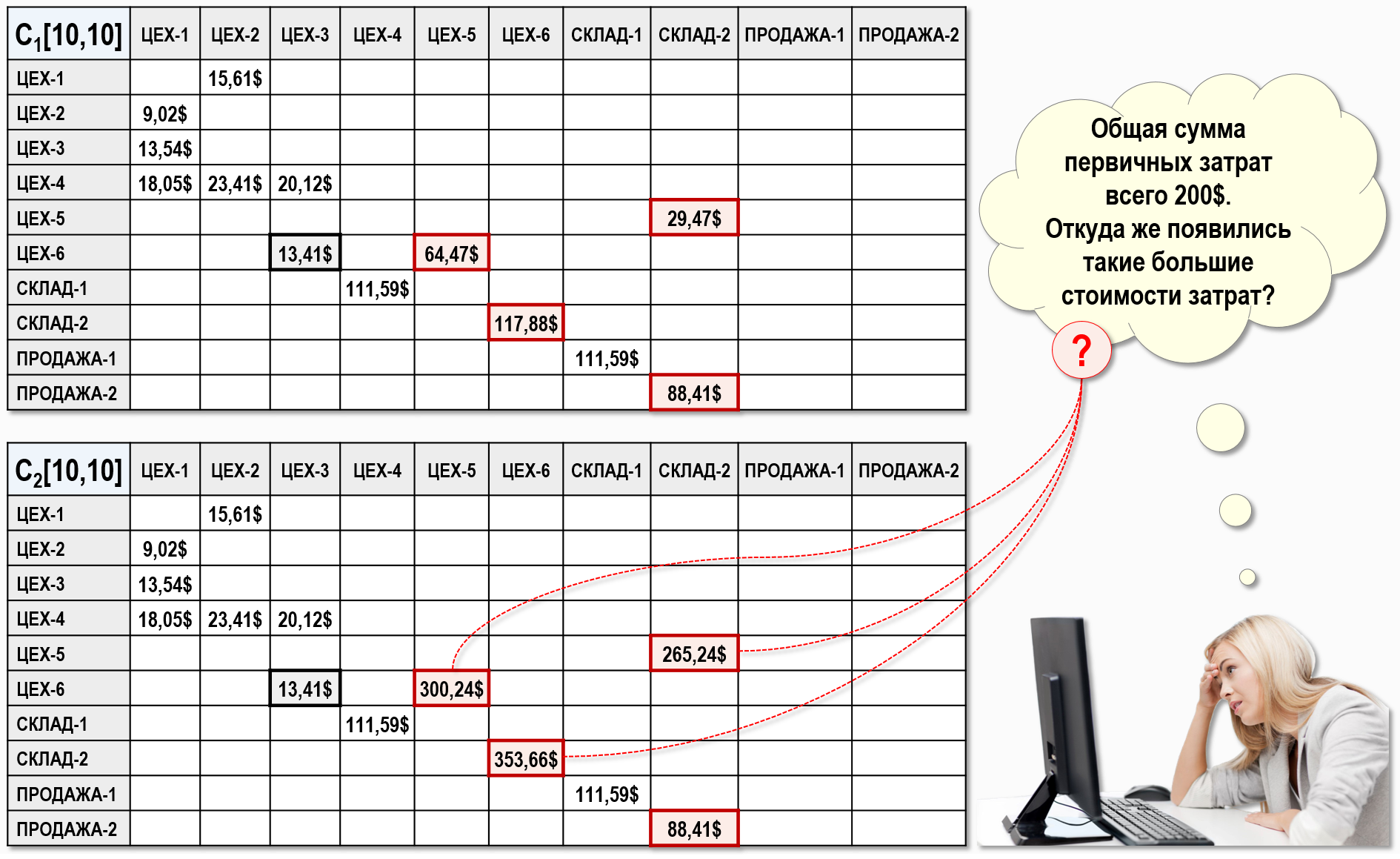
Решим СЛАУ и представим результаты расчета себестоимости с помощью двух матриц стоимостей: C1[10,10] – для первого варианта и C2[10,10] – для второго варианта:
Как видно на рисунке, результаты расчетов для второго сценария производственной программы несколько необычны – некоторые стоимости вторичных затрат значительно превысили общую стоимость всех(!) первичных затрат предприятия (200$).
Это действительно интересная особенность модели для расчета себестоимости на основе взвешенной оценки стоимости. В данном случае общая стоимость первичных затрат всех шести цехов предприятия для обоих вариантов производственной программы, т.е. общая стоимость реальных ресурсов предприятия, использованных в производственном процессе, составила 200$ (зарплата, материалы, амортизация и т.п.). В процессе расчета себестоимости эта стоимость первичных затрат должна просто перераспределиться между узлами модели вслед за движением количества единиц калькуляции (шт, кг, ч, м-ч, кВт·ч, куб.м) и казалось бы, никак не может превысить стоимость первичных затрат. Но, оказалось, что данная математическая модель работает по-другому – единственное решение СЛАУ выглядит так, как это показано выше на рисунке. Если бы использовалась скользящая оценка стоимости, т.е. учитывалась бы хронологическая последовательность хозяйственных операций, то такого результата мы конечно бы не получили.
Но на самом деле, в этом нет ничего страшного, т.к. нас в итоге интересуют конечные сальдо счетов учета (узлов), в то время, как операции (дуги) показывают только изменения стоимостей по дебету и по кредиту счетов учета. В нашем примере ни в одном из цехов предприятия в конце периода не должно остаться затрат в незавершенном производстве, а на складах не должно остаться готовой продукции, т.е. для обоих вариантов все 200$ первичных затрат в итоге должны перейти в себестоимость проданной продукции. Проверим, так ли это.
Вариант 1:
111,59$ – себестоимость продукции, проданной со Склада-1 (10шт)
88,41$ – себестоимость продукции, проданной со Склада-2 (15кг)
111,59$+88,41$=200$ – общая себестоимость проданной продукции
Вариант 2:
111,59$ – себестоимость продукции, проданной со Склада-1 (10шт)
88,41$ – себестоимость продукции, проданной со Склада-2 (5кг)
111,59$+88,41$=200$ – общая себестоимость проданной продукции
Как видим, все стоимости первичных затрат (200$) в итоге перешли в себестоимость проданной продукции. Разница только в том, что в первом варианте со Склада-2 было продано 15кг продукции с себестоимостью 88,41$, а во втором варианте та же себестоимость соответствует 5кг проданной продукции, что и понятно, т.к. во втором варианте больше продукции со Склада-2 было использовано в процессе производства, что в итоге увеличило себестоимость каждого килограмма проданной со Склада-2 продукции.
Таким образом, наличие встречных затрат «очень» большой стоимости является для данной математической модели вполне нормальным явлением, только нужно понимать, что стоимости вторичных затрат в данном случае являются расчетными величинами, помогающими определить конечное сальдо счетов учета, и не всегда их можно рассматривать в качестве «реальных» стоимостей ресурсов предприятия.
Представим также результаты расчета в графической форме и посмотрим, как выглядят для нашего примера бюджеты затрат Цеха-5 и Цеха-6.
Как видим, бюджеты затрат первого и второго варианта довольно существенно различаются между собой, но таковы особенности данной модели для расчета себестоимости. И как мы уже говорили выше, избежать этих особенностей можно только в случае использования другой модели – на основе скользящей оценки стоимости, если это возможно, конечно. Тем же пользователям, которые используют модель для расчета себестоимости на основе взвешенной оценки стоимости (т.е. с помощью решения СЛАУ), остается только изучать особенности именно этой модели.
В частности, если посмотреть, как выглядит себестоимость произведенной продукции, т.е. себестоимость продукции на выходе Цеха-4 и Цеха-6, то даже в первом варианте мы увидим, что:
111,59$ – себестоимость продукции, произведенной Цехом-4 (10шт)
117,88$ – себестоимость продукции, произведенной Цехом-6 (20кг)
111,59$+117,88$=229,47 $ – общая себестоимость произведенной продукции
Даже в первом варианте общая себестоимость произведенной продукции превышает общую стоимость первичных затрат предприятия (200$), просто это не так бросается в глаза, как при втором варианте сценария производственной программы предприятия. Это произошло потому, что узел Цех-6 входит в контур встречных затрат, а в контуре стоимости затрат рассматриваются как расчетные, а не как «реальные» стоимости ресурсов предприятия. Еще раз подчеркнем, что это особенность математической модели расчета себестоимости на основе взвешенной оценки стоимости, которую надо учитывать, в том числе и в процессе составления бюджетов затрат.
Очень часто составление прогнозных бюджетов затрат для отдельных подразделений предприятия производится без учета целостности модели предприятия – в эти бюджеты затрат включаются планируемые величины первичных затрат и некая стоимость так называемых накладных расходов, т.е. стоимость вторичных затрат. Причем стоимость накладных расходов берется просто исходя из какого-либо норматива и считается неизменной для разных периодов. При таком подходе модель предприятия как бы «разрывается» на почти независимые друг от друга части. Использование же Графа затрат позволяет реализовать при планировании себестоимости так называемый принцип холизма (единства), устанавливающий, что деятельность ни одной части предприятия нельзя эффективно планировать, если делать это независимо от остальных частей, т.е. деятельность всех частей предприятия следует планировать одновременно и во взаимозависимости.
Что можно сказать в заключение статьи? Только то, что не все так просто в бухгалтерском учете, как кажется некоторым бухгалтерам и (увы) программистам. Скольких бы недоразумений можно было бы избежать, если бы обсуждение сложных методологических вопросов учета происходило бы с использованием математических моделей, а не на основе неких субъективных представлений специалистов. Причем, часто речь идет даже не о каких-то новых моделях, хотя бы применяли те, которые уже давно де-факто используются всеми учетными специалистами (как выше в статье). Но к сожалению, на эти модели просто не обращают внимания, считая, что безо всяких моделей знают, как должно быть «по-настоящему». Фигурально выражаясь, такие понятия, как «большая половина» и «меньшая половина» существуют только в обыденном сознании человека, с математической же точки зрения — это нонсенс, поэтому в профессиональной деятельности желательно руководствоваться все-таки математическими моделями.