В двух предыдущих статьях – Бухгалтерский учет и теория графов и Граф предприятия и Граф затрат мы выяснили, что в основе математической модели любой системы бухгалтерского учета, основанной на двойной записи, лежит такой математический объект, как граф, а точнее – ориентированный граф или орграф, который мы назвали Графом предприятия. Также мы выяснили, что в Графе предприятия можно выделить очень важный фрагмент (подграф), который используется для калькулирования себестоимости продукции, работ и услуг предприятия. Этот подграф мы назвали Графом затрат.
Теперь посмотрим, каким образом Граф затрат используется для калькулирования себестоимости, т.е. каким образом решается задача «закрытия» затрат на Графе затрат. Для этого опять обратимся к примеру из предыдущей статьи Граф предприятия и Граф затрат.
Пример. Предприятие состоит из трех цехов и офиса, в котором сосредоточен управленческий персонал. Цех 3 производит продукцию, а цех 1 и цех 2 являются цехами вспомогательного производства. На предприятие от двух поставщиков поступили материально-производственные запасы (МПЗ), за которые было оплачено с расчетного счета в банке. Поступившие МПЗ были использованы в производственном процессе. Работникам цехов и офиса была начислена и выплачена заработная плата. Продукция была продана покупателю, который оплатил за нее денежные средства на расчетный счет предприятия. Также денежные средства были перечислены с расчетного счета предприятия в одном банке на расчетный счет предприятия в другом банке.
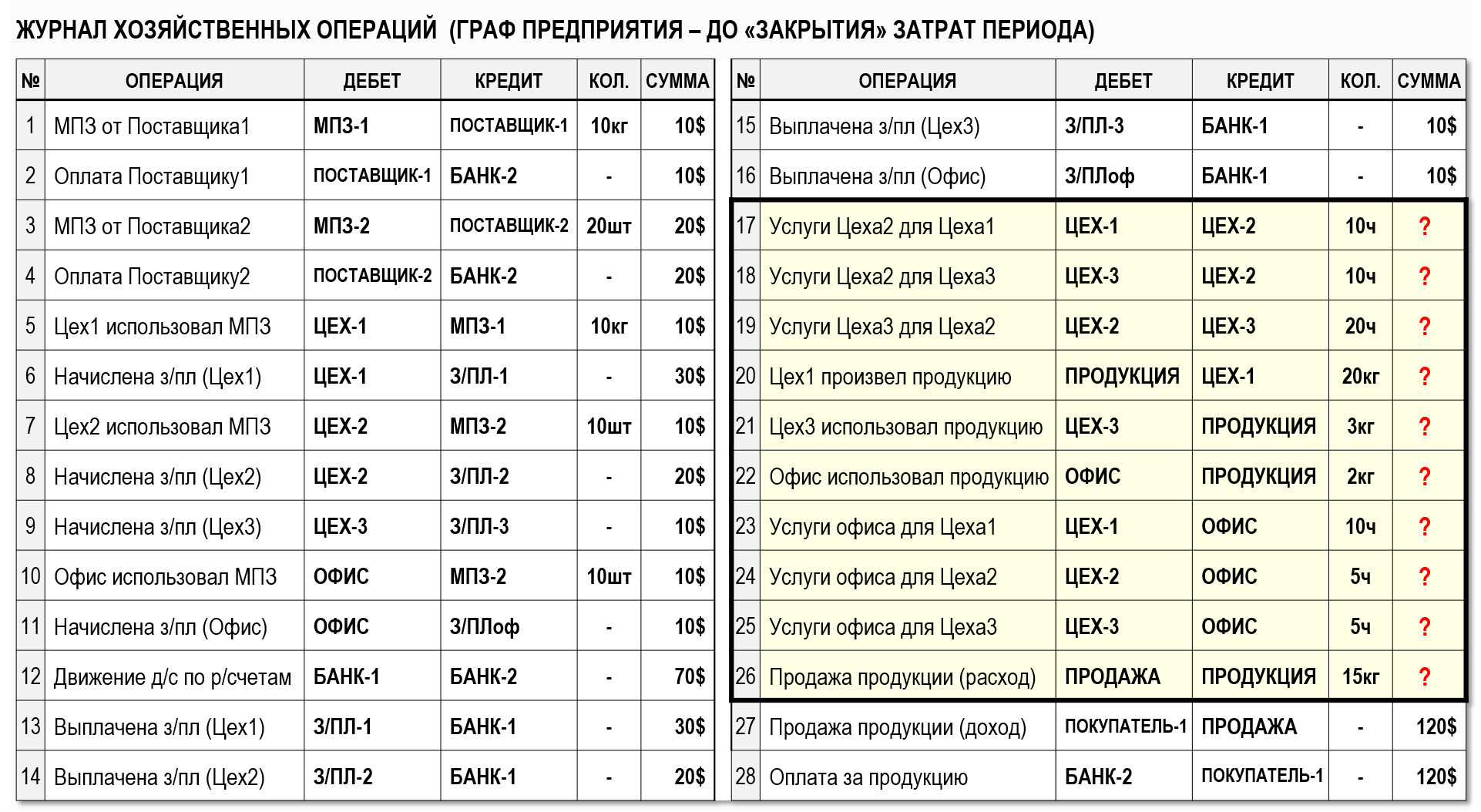
Представим хозяйственные операции за рассматриваемый период в журнале хозяйственных операций (ЖХО). В данном случае еще не была выполнена процедура «закрытия» затрат периода, поэтому стоимости операций с №17 по №26 пока не определены:
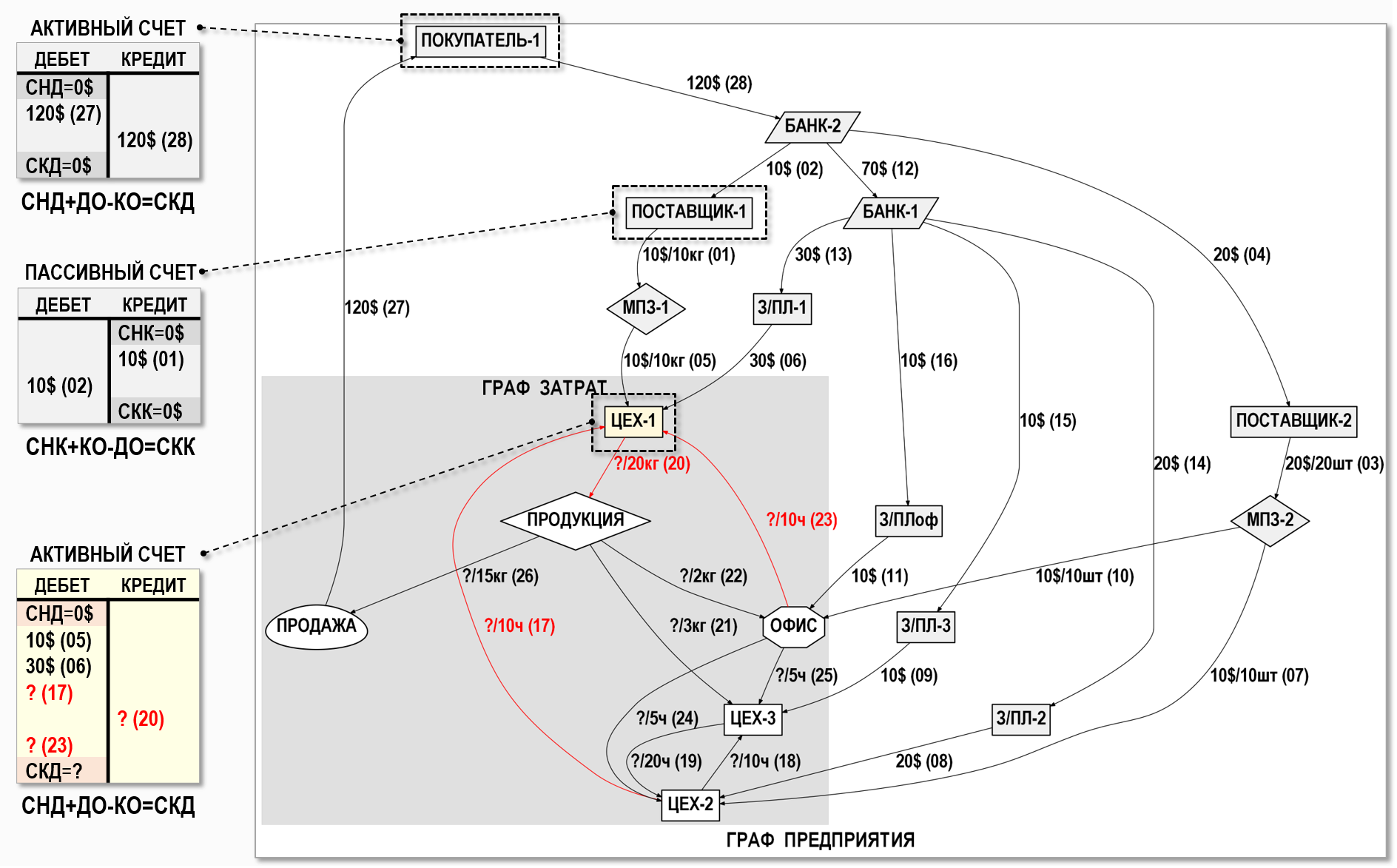
Представим также эти хозяйственные операции в графической форме – в виде взвешенного орграфа.
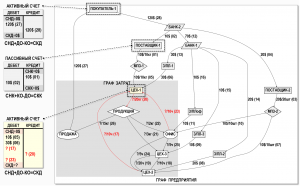
Как известно, для каждого счета бухгалтерского учета, т.е. для каждого узла Графа предприятия в обязательном порядке должно выполняться свое балансовое уравнение – как для активных, так и для пассивных счетов учета (примеры показаны выше на рисунке):
СНД+ДО–КО=СКД – для активных счетов учета
СНК+КО–ДО=СКК – для пассивных счетов учета
где:
СНД и СКД – сальдо начальное и конечное дебетовое
СНК и СКК – сальдо начальное и конечное кредитовое
ДО и КО – дебетовый и кредитовый обороты
Понятно также, что общее число таких балансовых уравнений должно быть равно числу счетов учета в бухгалтерской модели предприятия, т.е. числу узлов Графа предприятия. В теории графов общее число узлов графа называется его порядком – в данном случае порядок Графа предприятия равен 17-ти.
Поскольку счета учета попарно связаны между собой отношениями двойной записи, то понятно также, что и соответствующие им балансовые уравнения тоже должны быть «связаны» между собой, поскольку сумма любой хозяйственной операции одновременно используется сразу в двух балансовых уравнениях для корреспондирующих счетов учета. Это позволяет рассматривать всю совокупность балансовых уравнений Графа предприятия в качестве системы балансовых уравнений, которые должны выполняться одновременно – этот очевидный факт, собственно, лежит в основе математической модели системы бухгалтерского учета, основанной на двойной записи.
Как видно на рисунке, балансовые уравнения для счетов учета можно разделить на две группы – группу балансовых уравнений, моделирующих работу счетов учета в пределах границ Графа затрат, а также группу балансовых уравнений для счетов учета за его границами, и между этими двумя группами балансовых уравнений есть существенная разница.
Для всех счетов учета за пределами границ Графа затрат суммы хозяйственных операций по дебету и по кредиту всегда можно определить в момент отражения таких операций в системе бухгалтерского учета, например, из первичных учетных документов – товарных накладных, актов выполненных работ, банковских выписок или ведомостей начисления амортизации, заработной платы и т.п., а также с помощью методов ФИФО, ЛИФО и по средней себестоимости при выбытии материально-производственных запасов со склада. Это значит, что составить балансовые уравнения для таких счетов учета в любой момент времени не представляет труда, поскольку известны значения всех входящих в них величин.
Для счетов учета из Графа затрат ситуация сложнее – суммы некоторых хозяйственных операций с участием таких счетов учета нельзя определить непосредственно в момент отражения таких операций в системе бухгалтерского учета, эти суммы определяются расчетным путем в процессе выполнения процедуры «закрытия» затрат периода. Это значит, что значения всех величин, необходимых для составления балансового уравнения, которое в данном случае можно называть уравнением баланса затрат, мы сможем получить только после расчета себестоимости продукции (работ, услуг).
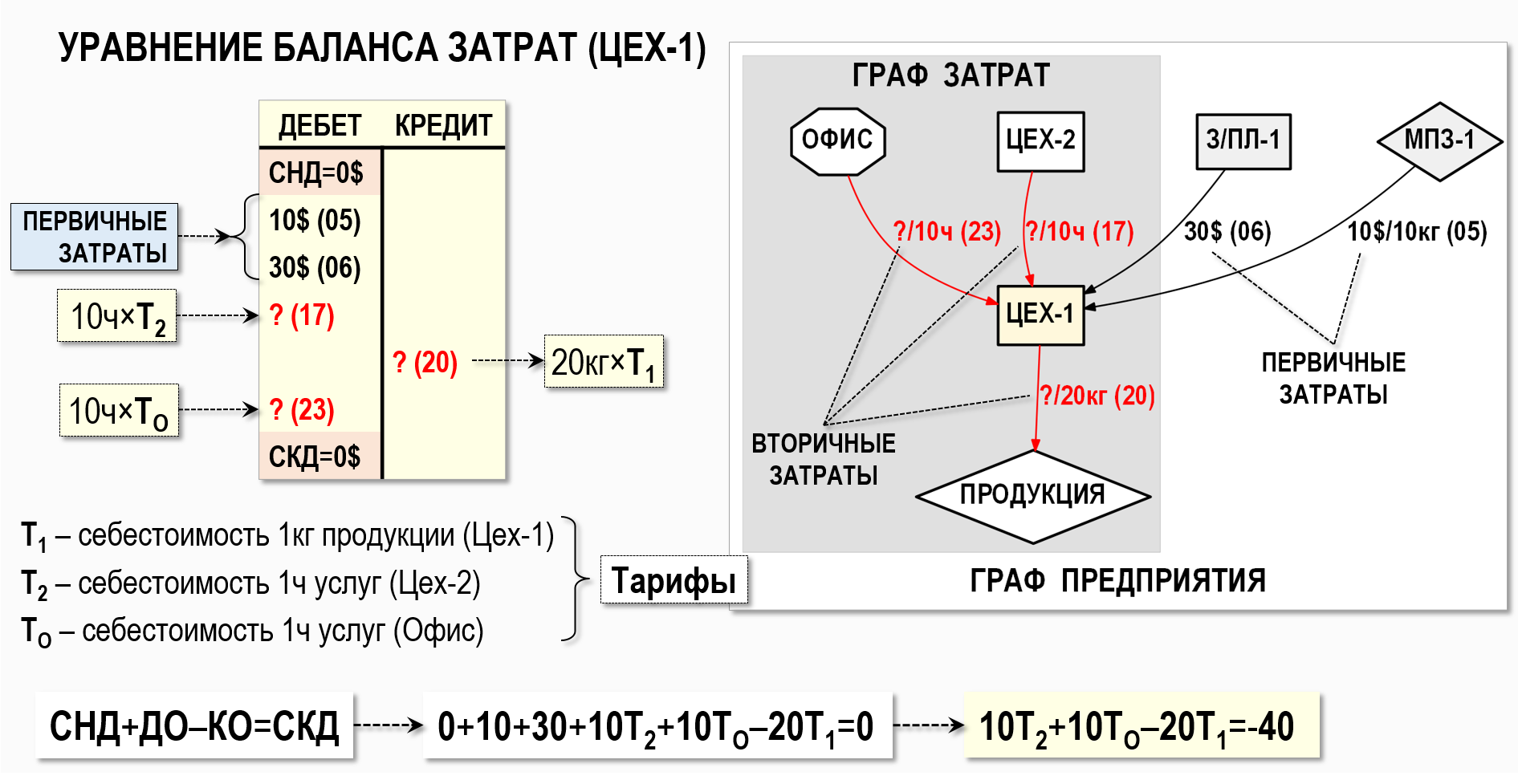
Действительно, когда происходит, например, выпуск готовой продукции на склад предприятия, то в соответствующем документе, назовем его Производственный отчет, мы можем указать только количество произведенной продукции, а ее себестоимость уже необходимо будет рассчитать. В качестве примера выше на рисунке выделен активный счет учета затрат «Цех-1», для которого известны суммы только двух хозяйственных операций №05 и №06 по дебету, а суммы остальных хозяйственных операций по дебету (№17 и №23) и по кредиту (№20) необходимо определить расчетным путем в процессе «закрытия» затрат периода. Похожая ситуация имеет место и для остальных счетов учета, входящих в Граф затрат.
Как же определить неизвестные суммы хозяйственных операций, входящие в уравнения баланса затрат для всех счетов учета в границах Графа затрат?
Ответ понятен – надо объединить все уравнения баланса затрат для таких счетов учета в систему уравнений и решить ее. Но для этого сначала необходимо немного модифицировать общий вид балансового уравнения для счетов учета из Графа затрат, добавив в него важное дополнительное условие, которое рассмотрим подробнее.
Вырежем из Графа предприятия фрагмент, моделирующий все хозяйственные операции (№05,06,17,20,23), в которых задействован счет учета «Цех-1»:
Используя терминологию теории графов можно сказать, что узел «Цех-1» и все входящие в него и исходящие из него дуги инцидентны, а все остальные счета учета на рисунке являются для узла «Цех-1» смежными (соседними) узлами. Четыре входящих дуги (№05,06,17,23) соответствуют хозяйственным операциям по дебету счета учета «Цех-1», исходящая дуга №20 – по его кредиту.
Составим уравнение баланса затрат для узла «Цех-1», причем для простоты будем пока считать, что на начало и на конец рассматриваемого периода в цехе 1 отсутствуют затраты в незавершенном производстве, т.е. СНД=0 и СКД=0. Это значит, что для составления уравнения баланса затрат необходимо определить только дебетовые и кредитовые обороты – ДО и КО. Более сложные варианты мы обсудим в последующих статьях, а пока нужно понять общий принцип составления уравнения баланса затрат.
Смысл «модификации» балансового уравнения для счетов учета, входящих в Граф затрат, состоит в том, что их кредитовые(!) обороты представляются в виде произведения количества продукции (работ, услуг) и себестоимости единицы продукции (работ, услуг). Далее единицу измерения продукции (работ, услуг) будем называть единицей калькуляции, а себестоимость одной единицы калькуляции будем называть тарифом.
Для узла «Цех-1» сумму хозяйственной операции №20 в этом случае можно представить в виде:
КО=20кг×Т1
где: Т1 – себестоимость 1-го кг продукции (тариф), произведенной цехом 1 в рассматриваемом периоде
Экономический смысл такого представления суммы операции именно по кредиту счета учета затрат «Цех-1» понятен и состоит в том, что цех 1 производит продукцию (20кг) и нам необходимо определить ее себестоимость, а хозяйственная операция по выпуску продукции на склад предприятия как раз и отражается по кредиту счета учета затрат «Цех-1». Поскольку предполагается, что количество произведенной продукции должно быть известно, например, из такого учетного документа, как Производственный отчет, то, определив тариф Т1 можно далее найти и себестоимость всех 20-ти кг продукции. Таким образом, введенное выше дополнительное условие для цеха 1 позволяет свести задачу расчета себестоимости продукции к задаче определения тарифа Т1.
А как же быть с дебетовыми оборотами для счета учета затрат «Цех-1»? Здесь существуют два варианта:
вариант 1 — суммы хозяйственных операций №05 и №06 нам уже известны (это стоимости первичных затрат), поэтому они просто подставляются в уравнение баланса затрат для узла «Цех-1»
вариант 2 — суммы хозяйственных операций №17 и №23 пока неизвестны (это вторичные затраты), но они пришли с кредита счетов учета «Цех-2» и «Офис» соответственно, и поэтому их можно представить в следующем виде:
операция №17 → 10ч×Т2
операция №23 → 10ч×ТО
где:
Т2 — себестоимость 1-го часа услуг (тариф) цеха 2
ТО — себестоимость 1-го часа услуг (тариф) офиса
Поскольку кредитовые обороты счетов учета затрат «Цех-2» и «Офис» также представлены в виде произведения количества услуг и соответствующего тарифа, то при корреспонденции этих двух счетов учета затрат со счетом учета затрат «Цех-1» в дебет этого счета учета поступают суммы хозяйственных операций, также выраженные в виде соответствующих произведений.
Другими словами, если кредитовый(!) оборот каждого входящего в Граф затрат счета учета представить в виде произведения количества продукции (работ, услуг) и тарифа, то автоматически и все дебетовые обороты остальных счетов учета в Графе затрат также будут представлены аналогичными произведениями, поскольку поступающие в дебет счетов учета суммы хозяйственных операций приходят с кредита других счетов учета Графа затрат.
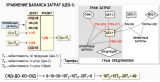
В результате, после небольшой цепочки очевидных преобразований, показанной выше на рисунке, уравнение баланса затрат для узла «Цех-1» примет следующий вид:
10Т2+10ТО–20Т1=-40
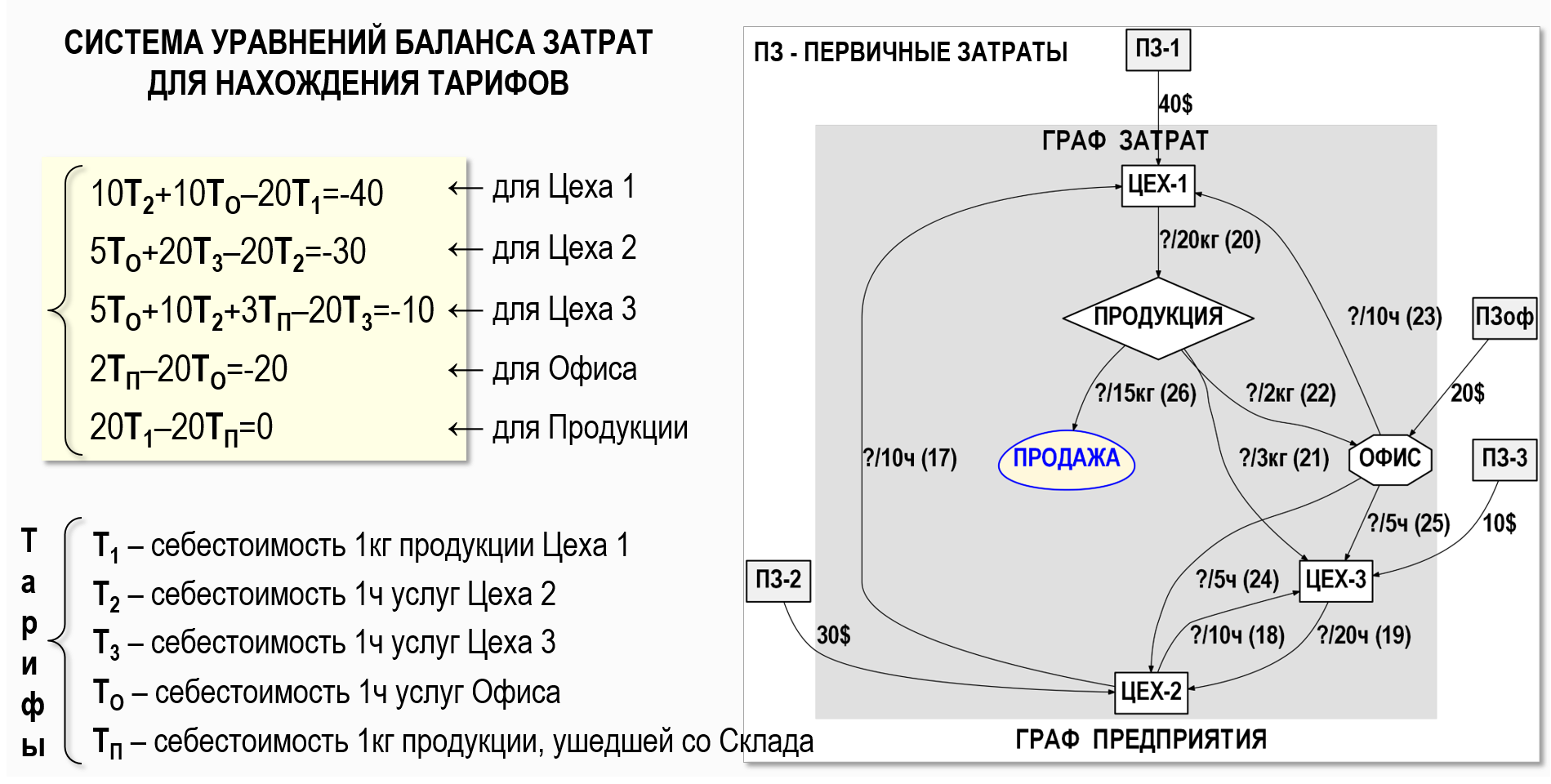
Это обычное линейное алгебраическое уравнение с тремя неизвестными – тарифами для узлов «Цех-1», «Цех-2» и «Офис». Для определения значений всех неизвестных тарифов необходимо составить аналогичные уравнения для остальных счетов учета, входящих в Граф затрат, объединить эти уравнения в систему линейных алгебраических уравнений (СЛАУ) и решить ее. Покажем для полноты картины СЛАУ для Графа затрат из нашего примера:
Данные уравнения баланса затрат составлены исходя из предположения о том, что у всех счетов учета отсутствуют начальные и конечные сальдо, т.е. на начало и на конец рассматриваемого периода отсутствуют затраты в незавершенном производстве и отсутствуют остатки готовой продукции на складе. Это учебный пример, поэтому усложнять его не имеет смысла. Более сложные ситуации можно посмотреть, например, в видеоролике Графы затрат. Варианты СЛАУ. Метод весовых коэффициентов или в следующих статьях.
Также следует обратить внимание на тот факт, что, хотя порядок Графа затрат равен 6-ти, но уравнений баланса затрат в СЛАУ всего только 5-ть. Это объясняется тем, что конечной или «финишной» точкой расчета себестоимости является дебет счета учета «Продажа», дебетовый оборот которого определяет себестоимость проданной продукции (аналог дебетового оборота счета учета 90.2 в российском плане счетов бухгалтерского учета). Кредитовый же оборот счета учета «Продажа» для целей расчета себестоимости значения не имеет, поскольку он отражает в системе бухгалтерского учета факт получения дохода от продажи продукции, т.е. формирует не расходную, а доходную часть операции продажи.
Это значит, что значение тарифа для счета учета «Продажа» находить не нужно, и в нашей задаче должно быть не 6-ть, а только 5-ть неизвестных тарифов, для нахождения значений которых достаточно 5-ти приведенных выше уравнений баланса затрат. Но следует учитывать, что счет учета «Продажа» все-таки важен для составления СЛАУ, т.к. сумма хозяйственной операции №26 с его участием формирует кредитовый оборот для счета учета «Продукция».
На этом, пожалуй, можно закончить данную статью, а также завершить весь вводный цикл из трех статей на тему Графов предприятий и Графов затрат. Автор надеется, что читатель получил общее представление об этих абстрактных бухгалтерских моделях.
В следующей статье мы начнем рассмотрение более специфических вопросов данной темы – рассмотрим матричную форму СЛАУ (опять для нашего примера), посмотрим, какие полезные матрицы можно использовать для решения задач на Графах затрат, а также поговорим о методах решения СЛАУ, в том числе решим СЛАУ, полученную в данной статье.