Метод Кларка-Райта. Оптимальное планирование маршрутов грузоперевозок

ВВЕДЕНИЕ

ПОСТАНОВКА ЗАДАЧИ

ПОДГОТОВИТЕЛЬНАЯ РАБОТА

ПОШАГОВОЕ ОПИСАНИЕ АЛГОРИТМА КЛАРКА_РАЙТА

ОПИСАНИЕ ПОСЛЕДОВАТЕЛЬНОГО РЕШЕНИЯ МЕТОДОМ КЛАРКА_РАЙТА

РЕЗУЛЬТАТЫ РЕШЕНИЯ

ВВЕДЕНИЕ.

Описанный метод используется в программе «Простое формирование маршрутов. Работа с картой. Расчет оптимальных вариантов доставки»

В статье «Оптимизация планирования доставки грузов. Алгоритм кластеризации k-means (метод K-средних)« было показано, КАК ПОЛУЧИТЬ ОПТИМАЛЬНЫЕ МАРШРУТЫ ДЛЯ ЗАДАННОГО КОЛИЧЕСТВА А/ТРАНСПОРТА из указанного места отгрузки, при этом грузоподъемность транспорта не принималась во внимание .
В этой статье покажем КАК УЗНАТЬ КОЛИЧЕСТВО НЕОБХОДИМОГО А/ТРАНСПОРТА С УЧЕТОМ ЕГО ГРУЗОПОДЪЕМНОСТИ ДЛЯ ФОРМИРОВАНИЯ ОПТИМАЛЬНЫХ МАРШРУТОВ.

Итак, поставлена задача отыскать самый выгодный маршрут движения транспорта, проходящий по одному разу через указанные пункты с последующим возвратом в исходный пункт (база). Критериями оптимальности в данной постановке задачи являются: минимальный пробег транспортного средства при максимальной загрузке кузова.

Сформулированная задача известна как «задача коммивояжера». Существует множество математических методов, позволяющих найти как точное, так и приближенное решение поставленной задачи. Среди методов, дающих точное решение, наиболее известны:

• «полный перебор»
• «метод ветвей и границ» 

Основным недостатком данных методов является высокая временная и емкостная сложность, что важно учитывать при большом количестве пунктов. Все эффективные (сокращающие полный перебор) методы решения «задачи коммивояжера» – методы эвристические. Из них наибольшее применение нашли:

• «метод генетических алгоритмов» 
• «метод Кларка-Райта» 
• «алгоритм муравьиной колонии» 
• «метод ближайшего соседа» 
• «метод включения ближайшего города» 
• «метод самого дешевого включения» 

Для решения нашей задачи наиболее приемлемым методом является метод Кларка-Райта. Он относится к числу приближенных, итерационных методов и может использоваться для компьютерного решения задачи развозки. Погрешность решения не превосходит в среднем 5–10 %. Достоинствами метода являются его простота, надежность и гибкость, что позволяет учитывать целый ряд дополнительных факторов, влияющих на конечное решение задачи.

Рассмотрим на примере, как применять метод Кларка-Райта. 

ПОСТАНОВКА ЗАДАЧИ.

Из исходного пункта, в котором располагается грузовой терминал (склад), необходимо доставить грузы 12 получателям. 

Таблица 1. Координаты и объем спроса получателей

Координаты грузового терминала (склада): x0 = 10, y0 = 15. Для доставки будет использоваться транспорт с максимальной грузовместимостью = 1500 шт.

ВОПРОС: Какое количество транспорта понадобится для развозки грузов ? Какая схема развозки будет оптимальной ?

ПОДГОТОВИТЕЛЬНАЯ РАБОТА.

Отметим эти точки в декартовой системе координат. Местоположение оптовой базы и 12 получателей, а также объем поставок каждому получателю приведены на рисунке 1. 

Рисунок 1. Расположение базы и пунктов доставки

Начальная схема маршрутов предполагает что для доставки груза каждому отдельному получателю организуется отдельный маршрут (см. рис. 2). Например, водитель загружает в кузов партию 450 шт. и везет ее в пункт 1, там разгружается, затем возвращается на базу, берет вторую партию 400 шт. и везет ее в пункт 2 и т.д. Таким образом, исходная схема развозки включает в себя только радиальные маршруты движения автомобиля, причем количество радиальных маршрутов совпадает с количеством получателей. В данном случае, схема развозки состоит из 12 радиальных маршрутов.

Рисунок 2. Начальная схема доставки груза

Суть метода заключается в том, чтобы, отталкиваясь от исходной схемы развозки, по шагам перейти к оптимальной схеме развозки с кольцевыми маршрутами. С этой целью вводится такое понятие, как километровый выигрыш.

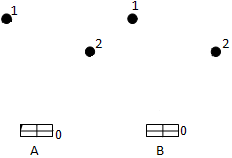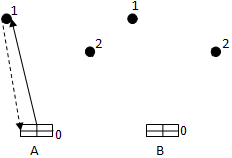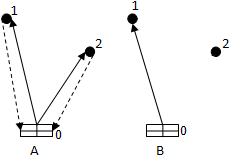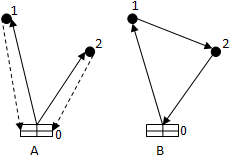
 Рисунок 3. Схемы доставки

На рисунке 3. отображены две схемы доставки. Схема доставки А (слева) обеспечивает доставку грузов в пункты 1 и 2 по радиальным маршрутам. В этом случае суммарный пробег автотранспорта равен:

 La = d01 + d10 + d02 + d20 = 2d01 + 2d02

Схема доставки B предполагает доставку грузов в пункты 1 и 2 по кольцевому маршруту. Тогда пробег автотранспорта составляет:

 Lв = d01 + d12 + d02

Схема В по показателю пробега автотранспорта дает, как правило, лучший результат, чем схема А. И поэтому при переходе от схемы А к схеме В получаем следующий километровый выигрыш:

 S12 = La — Lв = d01 + d02 — d12

В общем случае мы имеем километровый выигрыш:

 Sij = d0i + d0j — dij

где Sij – километровый выигрыш, получаемый при объединении пунктов i и j, км; d0i, d0j – расстояние между оптовой базой и пунктами i и j соответственно, км; dij – расстояние между пунктами i и j, км. 

 Полученные значения заносятся в таблицу 2., где представлены расстояния между пунктами dij (правая верхняя часть матрицы) и километровые выигрыши Sij (левая нижняя часть матрицы).

Таблица 2. Матрица расстояний и километровых выигрышей

Теперь вернемся к нашему примеру. Из табл. 1 возьмем данные:

• Пункт 0 (это база): x0 = 10, y0 = 15
• Пункт 1: х1 = 17, у1 = 15
• Пункт 2: х2 = 6, у2 = 15
• Пункт 3: x3 = 13, y3 = 3
• и т.д.

Рассчитаем расстояние d01 между пунктами 0 и 1 по формуле:

Аналогично получаем расстояние:

• для пунктов 0 и 2: d02 = 4
• для пунктов 0 и 3: d03 = 12,37
• для пунктов 1 и 2: d12 = 11
• для пунктов 1 и 3: d13 = 12,65
• для пунктов 2 и 3: d23 = 13,89
• и т.д

Потом для пунктов i и j получаем километровый выигрыш  Sij = d0i + d0j — dij:

• для пунктов 1 и 2: S12 = d01 + d02 — d12 = 7 + 4 — 11 = 0
• для пунктов 1 и 3: S13 = d01 + d03 — d13 = 7 + 12.37 — 12.65 = 6.72
• для пунктов 2 и 3: S13 = d02 + d03 — d23 = 4 + 12.37 — 13.89 = 2.48
• и т.д.

Полученные значения заносим в таблицу 3., где представлены расстояния между пунктами dij (правая верхняя часть матрицы) и километровые выигрыши sij (левая нижняя часть матрицы):

Таблица 3. Расчетная матрица расстояний и километровых выигрышей

Теперь, когда проведена вся необходимая подготовительная работа, приступим непосредственно к решению задачи.

ПОШАГОВОЕ ОПИСАНИЕ АЛГОРИТМА КЛАРКА-РАЙТА.

Демонстрация использования данного алгоритма применительно к рассматриваемой задаче приводится в табл. 4 и соответствующих комментариях к ней.

Шаг 1.

На матрице километровых выигрышей находим ячейку (i*, j*) с максимальным километровым выигрышем Smax:

При этом должны соблюдаться следующие три условия:

1. пункты i* и j* не входят в состав одного и того же маршрута;
2. пункты i* и j* являются начальным и/или конечным пунктом тех маршрутов, в состав которых они входят;
3. ячейка (i*, j*) не заблокирована (т.е. рассматривалась на предыдущих шагах алгоритма).

Если удалось найти такую ячейку, которая удовлетворяет трем указанным условиям, то переход к шагу 2. Если не удалось, то переход к шагу 6.

Шаг 2.

Маршрут, в состав которого входит пункт i*, обозначим как маршрут 1. Соответственно, маршрут, в состав которого входит пункт j*, обозначим как маршрут 2.

Введем следующие условные обозначения:

N = {1, 2, …, n} – множество получателей;

 – подмножество пунктов, входящих в состав маршрута 1;

 – подмножество пунктов, входящих в состав маршрута 2.

Очевидно, что  (согласно шагу 1, условие 1).

Рассчитаем суммарный объем поставок по маршрутам 1 и 2:

где qk – объем спроса k-го пункта, шт (см табл. 4).

Шаг 3.

Проверим на выполнение следующее условие:

где c – грузовместимость автомобиля, шт.

Если условие выполняется, то переход к шагу 4, если нет – к шагу 5.

Шаг 4.

Производим объединение маршрутов 1 и 2 в один общий кольцевой маршрут X. Будем считать, что пункт i* является конечным пунктом маршрута 1, а пункт j* – начальным пунктом маршрута 2. При объединении маршрутов 1 и 2 соблюдаем следующие условия:

• последовательность расположения пунктов на маршруте 1 от начала и до пункта i* не меняется;
• пункт i* связывается с пунктом j*;
• последовательность расположения пунктов на маршруте 2 от пункта j* и до конца не меняется.

Шаг 5.

Повторяем шаги 1-4 до тех пор, пока при очередном повторении не удастся найти Smax, который удовлетворяет трем условиям из шага 1.

Шаг 6.

Рассчитываем суммарный пробег автотранспорта.

ОПИСАНИЕ ПОСЛЕДОВАТЕЛЬНОГО РЕШЕНИЯ МЕТОДОМ КЛАРКА_РАЙТА.

Весь ход последовательного решения задачи представлен в таблице 4.

 Таблица 4. Ходы и промежуточные результаты решения задачи

Графа 1 – номер итерации.

Графы 2, 3 – номера пунктов i* и j*, которые обозначают ячейку с максимальным километровым выигрышем Smax = s(i*,j*), найденную в результате просмотра матрицы километровых выигрышей (см. табл. 3).

Графа 4 – значение максимального километрового выигрыша Smax.

Графы 5, 6 и 7 – результаты проверки условий 1, 2 и 3 при выполнении шага 1. “+” – положительный результат, “–” – отрицательный результат.

Графы 8 и 9 – объем перевозок по маршруту 1, в состав которого входит пункт i* (q1), и маршруту 2, в состав которого входит пункт j* (q2).

Графа 10 – проверка на условие , где c – грузовместимость транспортного средства. “+” – положительный результат проверки условия, “–” – отрицательный результат.

Графа 11 – порядковый номер кольцевого маршрута (всего в ходе решения получено всего четыре кольцевых маршрута, см. рис. 4).

Графа 12 – структура кольцевого маршрута, образовавшегося на данной итерации.

Рисунок 4. Графическое представление оптимальной схемы доставки

Рассмотрим, как происходит поэтапный поиск оптимального решения задачи. Начнем с того, что исходный план развозки состоит из 12 радиальных маршрутов, когда доставка груза в каждый из пунктов назначения осуществляется по отдельному маршруту (см. рис. 2). При этом общий пробег автотранспорта составляет (см. треугольную матрицу расстояний, табл. 3):

L0 = 2*d01 + 2*d02 + … + 2*d012 = 2*7.0 + 2*4.0 + 2*12.4 + 2*5.1 + … + 2*7.3 = 195 км.

 Теперь начнем пошаговый переход к новому оптимальному решению задачи, которое за счет объединения радиальных маршрутов в кольцевые позволит уменьшить суммарный пробег автотранспорта (графически это новое решение представлено на рис. 4).

Итерация 1.

• Объединяем два радиальных маршрута:  0-8-0 (объем доставки 200 шт.) и 0-3-0 (объем доставки 400 шт.) в общий кольцевой маршрут (под № 1) 0-8-3-0 (объем доставки 600 шт.). При этом суммарный пробег автотранспорта сокращается на 23,0 км.

Итерация 2.

• К кольцевому маршруту № 1– 0-8-3-0 (600 шт.) присоединяем радиальный маршрут 0-5-0 (150 шт.). При этом пункт 5 присоединяем к пункту 8, в результате чего получаем новую структуру кольцевого маршрута 0-5-8-3-0 (750 шт.). Суммарный пробег автотранспорта сокращается еще на 21,4 км. 
• Отметим важность соблюдения последовательности пунктов в кольцевом маршруте: именно 0-5-8-3-0, а не 0-5-3-8-0 или 0-8-3-5-0.
• Если i* = 8 и j* = 5, то после объединения они должны стоять на маршруте друг за другом.

 Итерация 3.

• Объединение пунктов 3 и 5 обеспечило бы выигрыш в 17,2 км. Но это объединение невозможно, поскольку оба пункта уже входят в состав кольцевого маршрута №1 – 0-5-8-3-0, а объединять можно пункты только из разных маршрутов. Таким образом, констатируем нарушение условия 1 и переходим к следующей итерации.

 Итерация 4.

• К кольцевому маршруту № 1 – 0-5-8-3-0 (750 шт.) присоединяем радиальный маршрут 0-12-0 (150 шт.). При этом пункт 12 присоединяем к пункту 3, в результате чего получаем новую структуру кольцевого маршрута 0-5-8-3-12-0 (1300 шт.). Суммарный пробег автотранспорта сокращается на 14,6 км.

 Итерация 5.

• Пункты 12 и 8 не объединяем, поскольку они уже входят в состав кольцевого маршрута 1 (нарушается условие 1).

 Итерация 6.

• Объединяем два радиальных маршрута:  0-1-0 (450 шт.)  и 0-11-0 (475 шт.) в общий кольцевой маршрут (под № 2) 0-11-1-0 (925 шт.). При этом суммарный пробег автотранспорта сокращается на 13,4 км.

 Итерация 7.

• Пункты 3 и 6 нельзя объединить по причине нарушения условия 2. Пункт 3 входит в состав кольцевого маршрута 1, и в этом маршруте он занимает «промежуточное» положение, то есть он связан с пунктами 8 и 12: 0-5-8-3-12-0. Радиальный маршрут 0-6-0 можно было бы присоединить к кольцевому маршруту 1 со стороны его «крайних» пунктов – 5 или 12, но к «промежуточным» пунктам 3 и 8 его присоединить нельзя.

 Итерации с 8 по 20

• Повторяют ту же логику рассуждений, что и в предыдущих 7 итерациях. Отметим только, что на итерациях 9, 11, 12, 16 и 18 объединение не производится только по причине нарушения условия 

 Итерации с 21 по 60

• Уже не имеют смысла, поскольку их выполнение уже не повлечет за собой изменение плана развозки.

Суммарный километровый выигрыш за 20 итераций составляет: 

S = 23,0 + 21,4 + 14,6 + 13,4 + 8,8 + 8,3 + 7,9 + 7,8 = 105,3 км 

 а общий пробег автотранспорта, соответственно:  

L1 = L0 – S = 195 –105,3 = 89,7 км

Графически оптимальная схема развозки представлена на рис. 4. Как видно, оптимальная схема развозки включает в себя четыре кольцевых маршрута (вместо первоначальных 12 радиальных маршрутов). Суммарный пробег автотранспорта можно также определить по следующей формуле:

, где Li – протяженность i-го маршрута, км; r – количество маршрутов.

 Рассмотрим, например, кольцевой маршрут 0-5-8-3-12-0. Протяженность маршрута определяется по формуле (см. табл. 4):

L1 = d0,12 + d12,3 + d3,8 + d8,5 + d5,0 = 7,3 + 5,1 + 4,1 + 5,4 + 12,0 = 33,9 км.

 Аналогично рассчитываем протяженность остальных маршрутов.

РЕЗУЛЬТАТЫ РЕШЕНИЯ.

Результаты решения задачисведены в таблицу: