Мультиинструментальный Brute Force

В одной из задач на Project Euler (здесь ссылка на русскую версию) предлагается найти простые 10-значные числа с повторениями. Под повторением понимаются не просто идущие подряд цифры, а все одинаковые цифры, которые встречаются в записи числа. Интересуют простые числа с максимальным количеством повторений. Для цифры 4 существует единственное простое число — 4444444447, в котором четверка повторяется 9 раз. Другим примером чисел, которые удовлетворяют условиям задачи, являются  7778777777 и 17777777777. Максимальное количество повторений семерки в 10-значном простом числе равно 9.

Оценим сложность задач. Для начала определим  размер области поиска, а именно, сколько существует простых чисел в диапазоне 10#k8SjZc9Dxk9…10#k8SjZc9Dxk10.  Для этого заглянем на сайт http://www.wolframalpha.com/ и в поле ввода наберем выражение primepi(10#k8SjZc9Dxk10)-primepi(10#k8SjZc9Dxk9). Функция primepi(x)  возвращает количество простых чисел,  не превосходящих х.

И так наши иголки мы будем искать в стоге из более чем 404 млн. простых чисел. Следующий вопрос — как эти числа получить?

Оказывается, есть люди, которым интересно разрабатывать программы для генерации простых чисел, более того они выкладывают свои разработки в открытом доступе.  Достижения автора поражают, его код работает черезвычайно быстро. Мы воспользуемся 64-х разрядным консольным приложением. Начнем с проверки количества простых чисел в интервале поиска. Ответ совпадает с полученным ранее, чего и следовало ожидать.

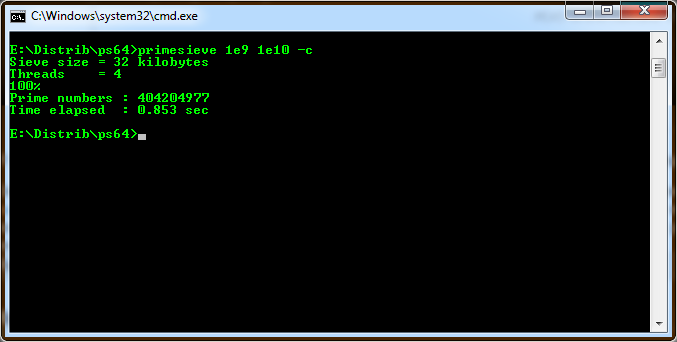
Это замечательное консольное приложение может находить простые числа в заданном диапазоне и сохранять их во внешний файл. На приведенном изображении мы ищем простые числа в интервале 4444444447,…4444444447+1 и выводим результат сначала на экран, затем в файл.

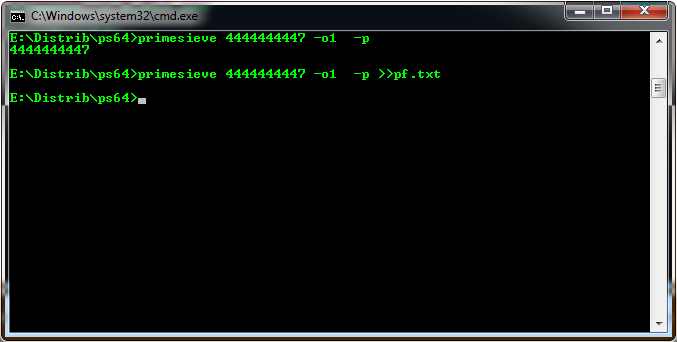
Если сохранить список чисел из диапазона поиска в одном файле, то он будет занимать на диске  4,51 Гб. При таких размерах приложение Блокнот отказывается  файл открывать. А ведь нам надо в дальнейшем обработать полученные числа. Поэтому будем выводить данные порциями с шагом 10#k8SjZc9Dxk8, начиная с 10*10#k8SjZc9Dxk8. Результаты сохраним не в текстовый файл, а в базу данных на SQL сервере. На первом шаге создадим в базе данных 90 таблиц  c именами  PrimeNumber10,PrimeNumber11,…,PrimeNumber99, которые содержат единственный столбец [output] с типом (nvarchar(10),NULL). Таблицы  сформируем с помощью простого кода в 1С.

for Num=10 to 99 do
Text="CREATE TABLE [dbo].[PrimeNumber"+num+"]([output] [nvarchar](10) NULL) ON [PRIMARY]";
adoConnect.Execute(Text);
enddo

Здесь adoConnect — это com-объект (COMОбъект(«ADODB.Connection»)).

На следующем шаге занесем набор простых чисел в наши таблицы. Сделать это можно спомощью такой команды:

Text="DECLARE @start sysname, @step sysname,@cmd sysname;
|
|SET @start='[Num]e8';
|SET @step='-o1e8';
|
|SET @cmd='...primesieve.exe '+@start+' +@step+' -p'
|
|delete from PrimeNumber[Num]
|
|Insert PrimeNumber[Num] (output)
|EXEC xp_cmdshell @cmd;";

[Num] — это параметр с номером таблицы. Команда выполняется на сервере, поэтому и консольное приложение для генерации простых чисел следует разместить там же. Кроме этого, в настройках сервера необходимо разрешить выполнение команды xp_cmdshell. Запускать вручную данный скрипт мы не будем, а призовем на помощь фоновые задания. Создадим общий модуль ФоновыеЗапросы и пропишем в нем следующую функцию:

Function  BackGroundQuery(Text) Export

adoConnect = new COMОбъект("ADODB.Connection");

ConnectString="Driver={SQL Server};Server=...;Database=...;Trusted_Connection=yes";

adoConnect.ConnectionTimeout = 1000;
adoConnect.CommandTimeout = 1000;
adoConnect.Open(ConnectString);

adoConnect.Execute(Text);

adoConnect.Close();

EndFunction 

Функция черезвычайно проста, единственное что она делает — отправляет на сервер команду, которую надо выполнить. А теперь оформим ее вызов.

for i=10+iStart to 99 do
query=СтрЗаменить(Text,"[Num]",i);
param=new array;
param.Add(query);
UID=new УникальныйИдентификатор;
mKey=строка(UID);
BgTask=ФоновыеЗадания.Execute(
"ФоновыеЗапросы.BackGroundQuery",
param,mKey,
"Fill prime table i="+i);
i=i+9;
enddo;

Какой бы ни был мощный сервер,  и его можно «подвесить». По этой причине я заполнял таблицы порциями по 9 штук, что и отражено в приведенном фрагменте.

Теперь, когда у нас есть исходные данные, можно приступить к извлечению нужных чисел. Для этого воспользуемся поиском по маске через оператор LIKE.  Для цифры 0 маска будет единственная: ‘_00000000_’. При этом искать числа надо только в таблицах с номерами 10,20,30… Всего таких чисел 8. Они приведены ниже.

1000000007
1000000009
4000000007
4000000009
6000000001
6000000007
7000000001
9000000001

Как показали дальнейшие исследования, максимальное количество повторяющихся цифр равно либо 9, либо 8. В первом случае надо использоваь маски вида:

‘_NNNNNNNNN’

‘N_NNNNNNNN’

‘NN_NNNNNNN’

………………………………………………….

‘NNNNNNNNN_’

Здесь N — цифра в интервале 1..9. Причем для четных цифр остается одна единственная маска — ‘NNNNNNNNN_’.

Во втором случае количество возможных масок — 45. Данные маски потребовалось применять для цифр 2 и 8. Тот факт, что эти цифры четные, позволило уменьшить количество перебираемых вариантов. В таблице приведена статистика для всех цифр. Первый столбец содержит повторяющуюся цифру, второй- максимальное количество повторений, третий — количество простых 10-значных чисел c повторением указанной цифры.

Цифра	Кол-во повторений	Количество простых чисел
0	8	8
1	9	12
2	8	39
3	9	7
4	9	1
5	9	1
6	9	1
7	9	9
8	9	32
9	9	8

Полученное  в  результате изложенного мультиинструментального BRUTE FORCE метода значение суммы простых чисел с заданным свойством оказалось правильным и позволило автору увеличить счет решенных задач.

Разумеется, данный метод не является оптимальным. Учитывая то, что консольное приложение позволяет проверить число на простоту, эффективнее было бы генерировать числа-кандидаты и отбирать из них  те, которые являются простыми. Тем не менее, приведенный подход позволяет расширить свой арсенал   и сделать будущую работу более продуктивной.

Просматривая задачи из проекта Эйлер, я обнаружил еще одну проблему, которая успешно решается с помощью изложенного метода. Основная ударная сила — программа генерации простых чисел в нужном диапазоне. Получив список чисел из интервала, определяемого номером строки треугольника,мы можем построить матрицу для поиска простых троек. Приведу некоторые контрольные значения, которые я получил.

 

Номер строки треугольника	Сумма искомых чисел
20 000	17 399 896 193
50 000	232 499 865 696
100 000	549 999 566 882
200 000	8 980 000 676 761
500 000	98 375 000 264 623
1 000 000	463 999 977 061 648