Задача В. Франгена, расставить на шахматной доске 10 “белых” и 9 “чёрных” ферзей так, чтобы ни один из них не находился под ударом противника
5 ферзей появились не случайно. Это минимальное количество фигур, при которых задач имеет решение. Как и в задаче о 8 ферзях (//infostart.ru/public/198717/) в решении используется перебор с возвратом. Но есть и дополнительные приемы. Так количество сочетаний вычисляется с помощью метода динамического прграммирования. Кроме этого, используется процедура генерации сочетаний по k из N. При поиске решений предполагается, что фигуры расположены в разных колонках и разных строках. В программе пристутствует возможность найти нужное расположение в ручную. Пользователь может ограничить количество найденных решений, в целях уменьшения времени работы процедуры поиска.
Эта задача была предложена В. Франгеном в 1980 г. и получила специальный приз на международном шахматном конкурсе. Автор предложил расставить на шахматной доске 10 “белых” и 9 “чёрных” ферзей так, чтобы ни один из них не находился под ударом противника, и считал, что задание выполняется единственным образом .Впоследствие автор задачи нашел еще одно решение, но оказалось, что есть и третье.
В обработку добавлены дополнительные возможности, которые позволяют решать подобные задачи.
А именно, отображение количества свободных клеток и процедура поиска расположения ферзей, отталкиваясь от текущего, при котором количество свободных клеток превышает существующее.
В обработке реализован алгоритм поиска решений задачи о 9 ферзях.
Related Posts
Получение логина и пароля техподдержки 1С из базы
Класс для вывода отчета в Excel
Счет-фактура для УПП
Библиотека классов для создания внешней компоненты 1С на C#- Акт об оказании услуг (со скидками) — внешняя печатная форма для Управление торговлей 11.1.10.86
Прайс-лист с артикулом в отдельной колонке
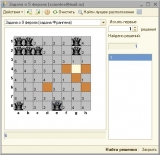
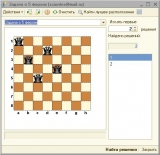
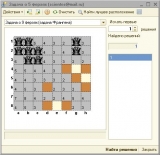
Долго искал в Сети эти самые три решения задачи Франгена. В конце концов нашел. С помощью обработки мне тоже удалось отыскать эти расстановки. Вопрос есть ли еще, пока открыт. Но в ближайшее время закроется.
Полный перебор позволил найти 24 решения. Но уникальных меньше, остальные получаются путем поворота доски.
3 решения. 24 получается поворотом доски — *4 варианта и отражением — *2.
Поскольку все фигуры, которые образуют искомое расположение лежат на одной половине доски, то перебор можно вести только по одной половине. Это резко сокращает время счета. Так для программы в 1С процедура поиска работала 3 мин. Было найдено 6 решений, уникальных, как и предполагалось, 3.