Продолжение публикации здесь (Алгоритмы поиска пути в графе. Часть 2)
Алгоритмы поиска пути чаще всего используют в играх, но бывает и такое infostart.ru/public/1081085, где автор применяет алгоритм поиска А* для нахождения коротких путей на складе.
Вот статья на тему реализации некоторых алгоритмов поиска, в частности А* (Перевод здесь). На платформе 1С 8.3 (далее просто 1С) реализация таких алгоритмов будет следующей:
&НаКлиенте
Функция Граф_ПоискВШирину(ВершинаКуда)
Очередь = Очередь_Новый();
Очередь_Добавить(Очередь, ВершинаКуда);
ПосещенныеВершины = Новый Структура;
ПосещенныеВершины.Вставить(ВершинаКуда, Новый Структура("Вершина, Стрелка", "А"));
Пока Не Очередь_Пустой(Очередь) Цикл
Вершина = Очередь_Получить(Очередь);
Соседи = Граф_ПолучитьСоседейВершины(Вершина);
Для каждого Сосед Из Соседи Цикл
Если Не ПосещенныеВершины.Свойство(Сосед.Ключ) Тогда
Очередь_Добавить(Очередь, Сосед.Ключ);
ПосещенныеВершины.Вставить(Сосед.Ключ, Новый Структура("Вершина, Стрелка", Вершина, Карта_ПолучитьСтрелкуРеверс(Сосед.Значение)));
КонецЕсли;
КонецЦикла;
КонецЦикла;
Возврат ПосещенныеВершины;
КонецФункции
Поиск в ширину с ранним выходом
&НаКлиенте
Функция Граф_ПоискВШиринуСРаннимВыходом(ВершинаКуда, ВершинаОткуда)
Очередь = Очередь_Новый();
Очередь_Добавить(Очередь, ВершинаКуда);
ПосещенныеВершины = Новый Структура;
ПосещенныеВершины.Вставить(ВершинаКуда, Новый Структура("Вершина, Стрелка", "А"));
Пока Не Очередь_Пустой(Очередь) Цикл
Вершина = Очередь_Получить(Очередь);
Если Вершина = ВершинаОткуда Тогда
Прервать;
КонецЕсли;
Соседи = Граф_ПолучитьСоседейВершины(Вершина);
Для каждого Сосед Из Соседи Цикл
Если Не ПосещенныеВершины.Свойство(Сосед.Ключ) Тогда
Очередь_Добавить(Очередь, Сосед.Ключ);
ПосещенныеВершины.Вставить(Сосед.Ключ, Новый Структура("Вершина, Стрелка", Вершина, Карта_ПолучитьСтрелкуРеверс(Сосед.Значение)));
КонецЕсли;
КонецЦикла;
КонецЦикла;
Возврат ПосещенныеВершины;
КонецФункции
&НаКлиенте
Функция Граф_ЖадныйПоиск(ВершинаКуда, ВершинаОткуда)
ПриоритетнаяОчередь = ПриоритетнаяОчередь_Новый();
ПриоритетнаяОчередь_Добавить(ПриоритетнаяОчередь, ВершинаКуда, 0);
ВершиныОткуда = Новый Структура(ВершинаКуда, Новый Структура("Вершина, Стрелка", "А"));
ВершинаЦель = Граф[ВершинаОткуда];
Пока Не ПриоритетнаяОчередь_Пустой(ПриоритетнаяОчередь) Цикл
Вершина = ПриоритетнаяОчередь_Получить(ПриоритетнаяОчередь);
Если Вершина = ВершинаОткуда Тогда
Прервать;
КонецЕсли;
Соседи = Граф_ПолучитьСоседейВершины(Вершина);
Для каждого Сосед Из Соседи Цикл
Если Не ВершиныОткуда.Свойство(Сосед.Ключ) Тогда
Приоритет = Граф_ПолучитьРасстояние(Граф[Сосед.Ключ], ВершинаЦель);
ПриоритетнаяОчередь_Добавить(ПриоритетнаяОчередь, Сосед.Ключ, Приоритет);
ВершиныОткуда.Вставить(Сосед.Ключ, Новый Структура("Вершина, Стрелка", Вершина, Карта_ПолучитьСтрелкуРеверс(Сосед.Значение)));
КонецЕсли;
КонецЦикла;
КонецЦикла;
Возврат ВершиныОткуда;
КонецФункции
&НаКлиенте
Функция Граф_АлгоритмДейкстры(ВершинаКуда, ВершинаОткуда)
ПриоритетнаяОчередь = ПриоритетнаяОчередь_Новый();
ПриоритетнаяОчередь_Добавить(ПриоритетнаяОчередь, ВершинаКуда, 0);
Дистанция = Новый Структура(ВершинаКуда, Новый Структура("Вершина, Стрелка", "А"));
СтоимостьДвижения = Новый Структура(ВершинаКуда, 0);
Пока Не ПриоритетнаяОчередь_Пустой(ПриоритетнаяОчередь) Цикл
Вершина = ПриоритетнаяОчередь_Получить(ПриоритетнаяОчередь);
Если Вершина = ВершинаОткуда Тогда
Прервать;
КонецЕсли;
Соседи = Граф_ПолучитьСоседейВершины(Вершина);
Для каждого Сосед Из Соседи Цикл
НоваяСтоимость = СтоимостьДвижения[Вершина] + Граф_ПолучитьСтоимость(Вершина);
ПрежняяСтоимость = Неопределено;
Если Не СтоимостьДвижения.Свойство(Сосед.Ключ, ПрежняяСтоимость)
Или НоваяСтоимость < ПрежняяСтоимость
Тогда
СтоимостьДвижения.Вставить(Сосед.Ключ, НоваяСтоимость);
Приоритет = НоваяСтоимость;
ПриоритетнаяОчередь_Добавить(ПриоритетнаяОчередь, Сосед.Ключ, Приоритет);
Дистанция.Вставить(Сосед.Ключ, Новый Структура("Вершина, Стрелка", Вершина, Карта_ПолучитьСтрелкуРеверс(Сосед.Значение)));
КонецЕсли;
КонецЦикла;
КонецЦикла;
Возврат Дистанция;
КонецФункции
&НаКлиенте
Функция Граф_АлгоритмА(ВершинаКуда, ВершинаОткуда)
ПриоритетнаяОчередь = ПриоритетнаяОчередь_Новый();
ПриоритетнаяОчередь_Добавить(ПриоритетнаяОчередь, ВершинаКуда, 0);
ВершиныОткуда = Новый Структура(ВершинаКуда, Новый Структура("Вершина, Стрелка", "А"));
СтоимостьДвижения = Новый Структура(ВершинаКуда, 0);
ВершинаЦель = Граф[ВершинаОткуда];
Пока Не ПриоритетнаяОчередь_Пустой(ПриоритетнаяОчередь) Цикл
Вершина = ПриоритетнаяОчередь_Получить(ПриоритетнаяОчередь);
Если Вершина = ВершинаОткуда Тогда
Прервать;
КонецЕсли;
Соседи = Граф_ПолучитьСоседейВершины(Вершина);
Для каждого Сосед Из Соседи Цикл
НоваяСтоимость = СтоимостьДвижения[Вершина] + Граф_ПолучитьСтоимость(Сосед.Ключ);
ПрежняяСтоимость = Неопределено;
Если Не СтоимостьДвижения.Свойство(Сосед.Ключ, ПрежняяСтоимость)
Или НоваяСтоимость < ПрежняяСтоимость
Тогда
СтоимостьДвижения.Вставить(Сосед.Ключ, НоваяСтоимость);
Приоритет = НоваяСтоимость + Граф_ПолучитьРасстояние(Граф[Сосед.Ключ], ВершинаЦель);
ПриоритетнаяОчередь_Добавить(ПриоритетнаяОчередь, Сосед.Ключ, Приоритет);
ВершиныОткуда.Вставить(Сосед.Ключ, Новый Структура("Вершина, Стрелка", Вершина, Карта_ПолучитьСтрелкуРеверс(Сосед.Значение)));
КонецЕсли;
КонецЦикла;
КонецЦикла;
Возврат ВершиныОткуда;
КонецФункции
Как могли заметить во всех алгоритмах используется абстактная структура данных Очередь, либо Приоритетная очередь. Как реализовать их в 1С можно почитать тут.
Выше описанная реализация возвращает направленные дуги в виде структуры, ключи которой будут вершины, а в значениях хранится направление следующей вершины. Таким образом, чтобы найти путь мы должны знать в какой вершине сейчас находимся и обратившись к полученной структуре находим вершину куда переместиться дальше. И так до тех пор пока есть куда перемещаться :).
Теоретические описания алгоритмов приводить не буду. Выделю главные, на мой взгляд, моменты:
Поиск в ширину говорит нам как посетить все вершины, поэтому его применение гораздо шире, чем поиск пути.
Жадный поиск использует расстояние до цели как критерий выбора следующей вершины.
Алгоритм дейкстры использует такое понятие как стоимость перемещения в следующую вершину, например, движение через препятствие может иметь повышенную стоимость прохождения. Поиск в ширину и жадный поиск считает, что стоимость перемещения одинакова.
Алгоритм А* использует такие понятия как стоимость перемещения и расстояние до цели (на самом деле эвристика может быть другой). Т.е. это жадный поиск и алгоритм дейкстры в одном.
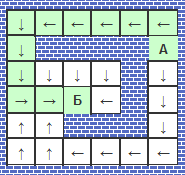
Для наглядности сделал обработку, которая выглядит так:
 Пример работы алгоритма А*:
Пример работы алгоритма А*:

Обработка сделана средствами платформы 1С 8.3.10 без использования внешних компонент. Карта, на которой отображается путь интерактивна т.е. можно мышкой переносить точки А и Б, ставить(убирать) стену, лес. Для алгоритмов А* и Дейкстры стоимость пути по лесу равна 3 единицам, по пустой ячейке 1.
Еще есть сайт где наглядно можно посмотреть и другие алгоритмы поиска пути.
UPD: Добавил волновой алгоритм
Волновой алгоритм визуально будет выглядеть как поиск в ширину с ранним выходом, только вместо стрелок будут указаны номера итерации (номера волн). А вот реализация будет отличаться, потому как на выходе получаем карту с волнами и по ней строим путь, выбирая соседа с наименьшим номером волны. Пока не дойдем до 0.
Волновой алгоритм — распространение волны
&НаКлиенте
Функция Граф_ВолновойАлгоритм_РаспространениеВолны(ВершинаКуда, ВершинаОткуда)
Очередь = Очередь_Новый();
Очередь_Добавить(Очередь, ВершинаКуда);
ПосещенныеВершины = Новый Структура;
ПосещенныеВершины.Вставить(ВершинаКуда, 0); // В значении храним номер волны
Пока Не Очередь_Пустой(Очередь) Цикл
Вершина = Очередь_Получить(Очередь);
Если Вершина = ВершинаОткуда Тогда
Прервать;
КонецЕсли;
НомерВолны = ПосещенныеВершины[Вершина];
Соседи = Граф_ПолучитьСоседейВершины(Вершина);
Для каждого Сосед Из Соседи Цикл
Если Не ПосещенныеВершины.Свойство(Сосед.Ключ) Тогда
Очередь_Добавить(Очередь, Сосед.Ключ);
ПосещенныеВершины.Вставить(Сосед.Ключ, НомерВолны + 1);
КонецЕсли;
КонецЦикла;
КонецЦикла;
Возврат ПосещенныеВершины;
КонецФункции
Волновой алгорити — восстановление пути
&НаКлиенте
Функция Граф_ВолновойАлгоритм_ВосстановлениеПути(ПосещенныеВершины, ВершинаОткуда)
НомерВолны = Неопределено;
Путь = Новый Массив;
ПриоритетнаяОчередь = ПриоритетнаяОчередь_Новый();
ПриоритетнаяОчередь_Добавить(ПриоритетнаяОчередь, ВершинаОткуда, 0);
Пока Не ПриоритетнаяОчередь_Пустой(ПриоритетнаяОчередь) Цикл
Вершина = ПриоритетнаяОчередь_ПолучитьБезУдаления(ПриоритетнаяОчередь);
Путь.Добавить(Вершина);
Если ПосещенныеВершины.Свойство(Вершина, НомерВолны) И НомерВолны = 0 Тогда // Достигли цели
Прервать;
КонецЕсли;
ПриоритетнаяОчередь = ПриоритетнаяОчередь_Новый();
Соседи = Граф_ПолучитьСоседейВершины(Вершина);
Для каждого Сосед Из Соседи Цикл
Если ПосещенныеВершины.Свойство(Сосед.Ключ, НомерВолны) Тогда
ПриоритетнаяОчередь_Добавить(ПриоритетнаяОчередь, Сосед.Ключ, НомерВолны);
КонецЕсли;
КонецЦикла;
КонецЦикла;
Возврат Путь;
КонецФункции
ПС: поскольку обработка выполнена в стиле автоматного программирования, то к ней идет спецификация, состоящая из схем связей и графов перехода (диаграмм состояний). Для полного тестирования требовалось лишь проверить поведение во всех состояниях по графу перехода. Тестирование проводилось интерактивно, для этого в обработке есть кнопка "Показать протокол тестирования". Список литературы по автоматному программированию и конечным автоматам:
[1] — http://is.ifmo.ru/books/_book.pdf — Н. И. Поликарпова, А. А. Шалыто. Автоматное программирование. СПб 2008.
[2] — http://is.ifmo.ru/automata/
[3] — http://softcraft.ru/auto/
 Пример работы алгоритма А*:
Пример работы алгоритма А*:






И не далее как пару недель назад : )))
Замечательно! Можно взять алгоритм не «выдумывая» его)))))
А как на счет волнового алгоритма?
хорошо, будет ли пример jump point search?
(5) Пока пас. Может быть позже.
Тогда еще спрошу. В случае если есть несколько точек Б интересно какая из них ближайшая. Какой из них предпочтительней?
(7) При поиске в ширину можно добавить несколько вершин, тогда функцию можно расширить так:
Показать
В результате мы получим карту с потоками до вершин. Т.е. зная вершину где мы находимся, используя такую карту мы сразу движемся в ближнюю точку (карта прикреплена ниже).
Если же необходимо предварительно знать размеры пути, то это будет похоже на волновой алгоритм, только волны будут расходиться от точки А, и поскольку там хранятся номера волн, то в каждой точке Б будет номер волны, и чем меньше номер, тем путь до точки Б ближе.
Но это не подойдет для жадного поиска и алгоритма А*.
ПС: Похоже надо делать продожение, где реализовать алгоритмом jump point search и возможность указывать множество точек Б.
Дельная вещь, однозначно в копилку, и плюс от меня.
(8) Точно!!! Про продолжение согласен.