Вычисление 200 тысяч знаков числа pi

28.05.2019 93 Comments

Математика и алгоритмы, Разработка

В статье рассматриваются возможности платформы выполнять сверхточные вычисления без использования сложных алгоритмов и внешних компонент на примере вычисления числа pi.

После прочтения статьи о недокументированной возможности добавления миллисекунд к дате (для тех, кто еще не знает, вот ссылка), задался вопросом: а что с числами? До какого предела точности мы можем вычислять результат?

Первое, что сразу пришло в голову — это попытаться определить машинное эпсилон, исходя из предположения, что представление числа в 1с это просто число с плавающей точкой, хранящееся как мантисса и показатель степени. В результате проверки обнаружилось, что предела деления как такового не существует.

При попытке вычисления программа просто зависает:

e = 1;
Пока 1 + e/2 > 1 Цикл
e = e/2;
КонецЦикла;
Сообщить(е);

Получается, что мы можем делать вычисления с неограниченной точностью, а точнее пока не закончится оперативная память.

Итак, проверим это. Возьмем произвольное число, например 23 и поделим его на 10 в степени 1000, прибавим к полученному результату 1.

а = 1 + 23*Pow(10, -1000);
Сообщить(а);   //1

Возвращается вроде единица без хвостика. Однако, это только кажется. Отнимем от результата 1, а после домножим то, что получилось обратно на 10#k8SjZc9Dxk1000:

а = 1 + 23*Pow(10, -1000);
Сообщить(а);   //1
Сообщить((а-1)*Pow(10, 1000));   //23

Наше число 23 никуда не пропало, оно хранилось в переменной а. Дробная часть, несмотря на ничтожную значимость по сравнению с целой частью, сохранилась.

Очевидно, что серьезная финансовая программа не может работать с такими стандартными типами как float и double и должна использовать тип, который обеспечивает поддержку десятичной арифметики с плавающей запятой (например, в java для этих целей используется тип BigDecimal, в Python тип Decimal). Получается, 1с предоставляет пользователю возможность рассчитывать себестоимость продукции с теоретически бесконечной точностью.

Однако, на вывод данных ограничения все же накладываются. Минимальное число (больше нуля), которое может отобразить программа это 10#k8SjZc9Dxk(-324). Не спрашивайте почему.

а = Pow(10,-324);
Сообщить(а); //0,000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000001
а = Pow(10,-325);
Сообщить(а); //0

Следовательно, мы можем производить различные математические вычисления с космической точностью. И это без всяких внешних компонент.

Теперь перейдем к теме и попробуем рассчитать число пи со сколь угодно малой погрешностью.

Сначала немного теории…

Один из самых простейших способов вычислить число пи — это использовать известную с начала XVIII века формулу Джона Мэчина:

 

 

 

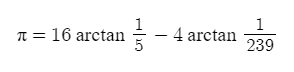
Самое замечательное в ней то, что арктангенс прекрасно раскладывается в ряд Тэйлора:

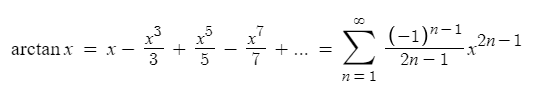
Переводим это в код:

Пи = 0;
Для Сч = 1 По 1000 Цикл
Зн = ?(Сч%2 = 0, -1, 1);
Ч = (Сч*2-1);
Пи = Пи + Зн*(16/(Ч*Pow(5,Ч)) - (4/(Ч*Pow(239,Ч))));
КонецЦикла;
Сообщить(Пи)  //3,141592653589793238462643383529999816173450437691564002130.......

И…. Сразу получаем… Всего 27 верных знаков после запятой.

Увеличение счетчика не приводит к точности вычислений.

Вы, конечно же, догадались в чем здесь проблема. Дело в том, что при делении, например, 1 на 3 выводится результат 0,333333333333333333333333333, ограниченный только 27 знаками. Можно ли обойти это ограничение? Оказывается, точность деления зависит от точности числителя дроби и следовательно, если мы добавим к нему очень малую величину, то результат будет вычислен с той же точностью.

Немного подправим код выше:

Пи = 0;
Ош = Pow(10,-2000);
Для Сч = 1 По 1000 Цикл
Зн = ?(Сч%2 = 0, -1, 1);
Ч = (Сч*2-1);
Пи = Пи + Зн*((16+Ош)/(Ч*Pow(5,Ч)) - ((4+Ош)/(Ч*Pow(239,Ч))));
КонецЦикла;

Далее попробуем сравнить точность полученного результата со справочным значением числа пи (первые 4 млн. знаков можно взять отсюда). Для этого будем извлекать по 10 знаков полученного числа в строку:

 //Число получено, но 1с отображает только 324 знака после запятой
//Выведем домножением остальные символы
ПиСтрокой = "3.";
Для Сч = 1 По 100 Цикл
ПиСтрокой = ПиСтрокой + Сред(Пи, 3,10);
Пи = Пи*Pow(10,10)%1;
КонецЦикла;

//Сравнение с оригиналом:
ПиОриг = "3.1415926535897932384626433832795028841971693993751058209749445923078164062862089986280348253421170679821480865132823066470938446095505822317253594081284811174502841027019385211055596446229489549303819644288109756659334461284756482337867831652712026091456485669234603486104543266482133936072602491412737245870066063155881748815209209628292540917153643678925903600113305305488204665213841469519415116094330572703657595919530921861173819326117931051185480744623799627495673518857527248912279381830119491298336733624406566430860213949463952247371907021798609437027705392171762931767523846748184676694051320005681271452635608277857713427577896091736371787214684409012249534301465495853710507922796892589235420269561121290219608640344181598136297747713099605187072113499999983729780499510597317328160963185950244594553469083026425223082533446850352619311881710100031378387528865875332083814206171776691473035982534904287554687311595628638823537875937519577818577805321712268066130019278766111959092164202689";
Сообщить("Пи оригинал: " + ПиОриг);
Сообщить("Пи вычислен: " + ПиСтрокой);

Для Сч = 3 По 1002 Цикл
Если Сред(ПиОриг, Сч, 1) <> Сред(ПиСтрокой, Сч, 1) Тогда
Прервать;
КонецЕсли;
КонецЦикла;
Сообщить("Точность вывода знаков после запятой: " + (Сч-3));//Точность вывода знаков после запятой: 1 000

В результате за 1 секунду мы получили 1000 верных знаков. Напомню: в конце XIX века Вильям Шенкс нашёл 707 знаков числа пи, потратив на это 20 лет своей жизни. Однако, в 40-х годах, с помощью первых появившихся ЭВМ, было выяснено, что в своих расчетах он допустил ошибку на 520-м знаке и дальнейшие его вычисления оказались неверными.

Далее попробуем вычислить больше знаков и воспользуемся для этого формулой Бэйли — Боруэйна — Плаффа, выраженной через отношение двух полиномов:

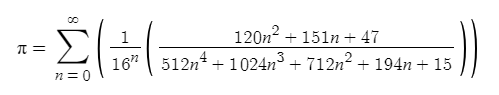
Код:

Пи = 0;
Ош = Pow(10,-10002);
Ст16 = 1;
Для Сч = 0 По 8298 Цикл
к1 = Сч;
к2 = к1*к1;
к3 = к2*к1;
к4 = к3*к1;

Числ = (120*к2+151*к1+47)+Ош;
Знам = (512*к4+1024*к3+712*к2+194*к1+15)*Ст16;
Ст16 =  Ст16 * 16;
Пи = Пи + Числ/Знам;
КонецЦикла;

После сравнения с оригиналом получаем за 25 секунд 10 000 верных цифр после запятой. Уже что-то.

И напоследок, нельзя не привести способ вычисления пи согласно безумной формуле братьев Чудновских (вдруг кому пригодится), с помощью которой они установили рекорд вычисления (на тот момент): 5 триллионов знаков после запятой! 

Но для этого нам понадобится изначально вычислить квадратный корень из числа 10005, входящий в формулу. Для этого воспользуемся итерационной формулой Герона.

а = 10005;  //Число из которого извлекам корень
КвКорень =sqrt(а);  //его начальное приближение
Ош = Pow(10,-300000);
Для Сч = 1 По 15 Цикл
КвКорень = (КвКорень+(а+Ош)/КвКорень)/2;
КонецЦикла;

И теперь вычислим пи методом Чудновских:

Пи = 13591409;
ak = 1;
k = 1;
Для Сч = 1 По 20010 Цикл
ak = (ak * -((6*k-5)*(2*k-1)*(6*k-1))+Ош)/(k*k*k*26680*640320*640320);
Пи = Пи + ak*(13591409 + 545140134*k);
k = k + 1;
КонецЦикла;
Пи = (Пи * КвКорень+Ош)/4270934400;
Пи = (1+Ош)/Пи;

В результате 283 789 точных знаков за 3 минуты! «У кого есть охота, пусть идёт дальше», как сказал когда-то Людольф ван Цейлен, вычислив 4 столетия назад 20 точных знаков числа пи после 10 лет упорной работы.

Спасибо, что дочитали до конца.

Related Posts

93 Comments

  1. Rise-s

    Познавательно

    Reply ↓
  2. ImPenguin

    Интересно! У вас там в тексте ошибочка, вы пишете что минимальное отображаемое число 10#k8SjZc9Dxk(-234), а в примере указываете -324

    Reply ↓
  3. Oleg_nsk

    (2) Спасибо. Поправил.

    Reply ↓
  4. user940969

    Любопытное исследование. Однозначно плюс.

    Reply ↓
  5. nomadon

    Какая разрядность платформы использовалась для экспериментов?

    Reply ↓
  6. SerVer1C

    Интересно. Но не всё так просто:

    а = 3 / 7;

    а = а + 1;

    результат = а * 7;

    Сообщить(Формат(результат, «ЧГ=»));

    напишет: 10,000000000000000000000000003

    И на будущее: не используйте 1с в алгоритмических расчетах, любой ЯВУ будет в ~10…100…1000 раз быстрее!

    Reply ↓
  7. Perfolenta

    (6) мелкая поправка: любой компилируемый язык будет быстрее, а с интерпретаторами не все так однозначно…

    тем более, если учесть разрядность чисел в 1с… не каждый интерпретатор имеет такие числа… например, OneScript не имеет… а тем более с такими не документированными возможностями, которые рассматриваются в этой статье…

    Reply ↓
  8. SerVer1C

    (7) Вы, наверное, ну щупали Python…

    Reply ↓
  9. scientes

    Любопытно. Я не знал, что 1с выполняет деление с точностью числителя. Пользовался собственной процедурой ДлинноеДеление. Оказывается, можно поступить проще.

    Reply ↓
  10. Oleg_nsk

    (5) х64

    Reply ↓
  11. Perfolenta

    (8) все там предсказуемо… стандартный Питон — обычный медленный интерпретатор (может чуть-чуть быстрее, чем 1С, но не критично), однако существуют реализации Питона имеющие JIT компилятор, которые вполне естественно работают на много быстрее…

    У интерпретаторов есть одна особенность. Скорость работы алгоритмов зависит от числа и качества библиотечных функций, которые интерпретатор использует при вычислениях…

    Reply ↓
  12. frkbvfnjh

    Оооочень круто, сам недавно делал эксперименты по расчету ПИ в 1С и выяснению максимальной точности чисел после запятой, но так далеко не зашел, не догадался, что в 1С с дробными числами так же все интересно как и с датами. Спасибо за публикацию!

    Reply ↓
  13. frkbvfnjh

    (9) А можете привести текст своей функции ДлинноеДеление? Очень интересно посмотреть.

    Reply ↓
  14. SerVer1C

    (11)

    стандартный Питон — обычный медленный интерпретатор (может чуть-чуть быстрее, чем 1С

    Откуда такая уверенность? Обоснуйте свой ответ, желательно, с пруфами.

    Reply ↓
  15. HEKPOH

    Респект и уважуха!!!

    Reply ↓
  16. DarkAn

    (13) Скорее всего (9) имеет ввиду Сокровище Рамануджана, я буквально на днях ознакомился с данной статьей, но тут действительно шагнули дальше, то есть глубже.

    Reply ↓
  17. scientes

    (16)Совершенно верно, в этой статье есть пример такой функции.

    Reply ↓
  18. Perfolenta

    (14) пруфов не нашел, хотя интернет забит статьями типа «почему Питон медленный»…

    попробовал протестировать сам… взял свой компилируемый Net язык, Python 3.5, и 1С 8.3.13.1644

    запустил вот этот код:

    n = 139
j = 0
while j < 100000:
j = j + 1
fib1 = 1
fib2 = 1
i = 0
while i < n — 2:
fib_sum = fib1 + fib2
fib1 = fib2
fib2 = fib_sum
i = i + 1
print(fib2)

    Показать

    и соответственно:

    n=139;
j = 0;
Пока j < 100000 Цикл
j = j + 1;
fib1 = 1;
fib2 = 1;
i = 0;
Пока i < n — 2 Цикл
fib_sum = fib1 + fib2;
fib1 = fib2;
fib2 = fib_sum;
i = i + 1;
КонецЦикла;
КонецЦикла;
Сообщить(fib2);

    Показать

    результат такой:

    компилируемый Net язык — 0,21 сек

    питон — 5,7 сек

    1С — 112 сек

    т.е. 1С действительно подтвердила, что она очень медленная, но и Питон показал, что он все таки не компилятор…

    Правда в этом тесте надо учесть,что разные языки используют разные числовые библиотеки… у 1С самые многоразрядные числа и она в них считает от начала и до конца.. А Питон судя по всему повышает разрядность чисел динамически по мере необходимости… мой язык считал в Net типе Decimal…

    Скажу честно, от 1с ожидал большего 🙂

    так что соглашаюсь с вами — Питон значительно быстрее 1с…

    Reply ↓
  19. scientes

    Вопрос на засыпку на собеседовании:

    «Вывести на печать значение дроби (1+1e-400)/)7»

    Reply ↓
  20. KEV8383

    Прям ностальгия по физмату )))

    Reply ↓
  21. starik-2005

    (18)

    Питон значительно быстрее 1с…

    А С быстрее любого другого языка, фактически (с О3 и march=native mtune=native). У меня множество Мандельброта 30FPS на Ryzen 1600 (3,4 Ггц) в 500×500 точек рендерится в один поток )))

    Reply ↓
  22. starik-2005

    (18)

    компилируемый Net язык — 0,21 сек

    вот в 10 раз больше вычислений на С.за 0,016 секунд на виртуальной машине на моем рабочем ноутбуке…

    Reply ↓
  23. starik-2005

    (18)

    компилируемый Net язык — 0,21 сек

    Вот под винду 1кк раз, т.е. в 10 раз больше вычислений:

    c:1>test.bat
Текущее время: 16:35:36,56
Введите новое время:
c:1>test.exe
fib=50095301248058389000000000000.000000
Текущее время: 16:35:36,70
Введите новое время:
c:1>

    Т.е. тут у нас 0,7-0,56 = 0,14 секунды, в принципе аналогично линуксовому времени.

    Reply ↓
  24. tsukanov

    А что если я скажу что тут меряются длинной арифметикой и кривой результат на double не особо интересен? )

    Reply ↓
  25. Perfolenta

    (23) кривой результат на Double мой компилируемый Net язык тоже в 10 раз быстрее делает…

    5,00953012480584E+28

    Время в секундах: 0,0219402

    на Си конечно можно писать более быстрые программы, чем на любом языке более высокого уровня, но и трудозатраты значительно больше… а на ассемблере еще быстрее, и труднее…

    Reply ↓
  26. starik-2005

    (25)

    а на ассемблере еще быстрее, и труднее…

    ну смотря что. Фиббоначчи на асме написать не труднее, но и скорость, полагаю, будет может быть раза в два всего быстрее за счет регистров, но, опять же, для 64-битных регистров для 139-го числа уже нехватит разрядов, поэтому придется юзать два 64-битных регистра (типа XAX+XDX. Сегодня до дома доберусь — проверю.

    Reply ↓
  27. starik-2005

    (24) у меня целочисленный вариант быстрее отрабатывает, но и 64 бит на 139-й фиббоначчи уже маловато. Поэтому целочисленной арифметикой тут мериться тоже смысла нет. А так — да, раза в 3 быстрее получается.

    Reply ↓
  28. starik-2005

    Кстати, только заметил, что винда меньше разрядов отдает для double, поэтому нолики на конце)))

    Reply ↓
  29. starik-2005

    Попробовал на асме — такая же скорость.

     mov rcx ,100000
l0:
push rcx

mov rcx ,138
mov rbx ,1
mov rax ,rbx
mov r8 ,0
mov r9 ,r8
l1:
add rax ,rbx
adc r8 ,r9
xchg rax ,rbx
xchg r8 ,r9
loop l1

pop rcx
loop l0

mov rbx,30
lea rsi,[msg]
l2:
sub rdx,rdx
mov rcx,10
div rcx

add dl,30h
mov [rsi+rbx],dl
dec rbx

or rax,rax
jnz l2

mov edx,msg_size
lea rsi,[msg]
mov edi,1  ; STDOUT
mov eax,1 ; sys_write
syscall

xor edi,edi ; exit code 0
mov eax,60 ; sys_exit
syscall

segment readable writeable

msg db ‘                                                  ‘,0xA
msg_size = $-msg

    Показать

    В итоге на моем домашнем iIntel® Core™ i7-2670QM CPU 0.036 секунд — и это больше, чем на моем рабочем i7-5500U на С++ (видимо из-за SSE — здесь просто целочисленная 128-битная арифметика, 64-битная быстрее на 0,005 сек).

    sergey$ time ./a00
4114278174457313509

real 0m0,036s
user 0m0,032s
sys 0m0,000s

    Не стал бодаться, чтобы все цифры вывелись — вывел только младшие 64 бита — вломы было )))

    Reply ↓
  30. Perfolenta

    (26) фибоначчи это не программа… это микропрограмма… 🙂

    Reply ↓
  31. Perfolenta

    (29)

    что-то результат у вас не понятный… вроде вот так должно быть:

    фиб(138) = 30 960 598 847 965 113 057 878 492 344

    фиб(139) = 50 095 301 248 058 391 139 327 916 261

    наверное на ассемблере все же сложнее 🙂

    Reply ↓
  32. starik-2005

    (31) так написал же, что только младшие 64 бита вывел.

    Reply ↓
  33. Perfolenta

    (32) я просто не понял как эти младшие разряды сопоставить с результатом… не видно ни каких совпадений…

    Reply ↓
  34. starik-2005

    Попробовал без цикла сделать, т.е. просто add,adc,xchg, xchg — и так 138 раз. И стало работать за 0,016-0,017 сек для 128 бит и за 0,010-0,011 для 64 бит. В принципе 80-битный double вполне себе укладывается в погрешность на уровне битности (0,016 за 80 бит vs 0,017 за 128 бит vs 0,011 за 64 бита).

    Reply ↓
  35. starik-2005

    (33)

    … не видно ни каких совпадений.

    Я на С++ 64-битное беззнаковое целое гонял — аналогичный результат.

    Reply ↓
  36. starik-2005

    (31)

    50 095 301 248 058 391 139 327 916 261

    101000011101110111011100101010100011100100011000110110000000000000000000000000000000000000000000 — последние 43 бита пустые, однако…

    Reply ↓
  37. Perfolenta

    (36) т.е. у вас получилось

    50 095 301 248 058 388 718 985 150 464

    вместо

    50 095 301 248 058 391 139 327 916 261

    где-то намутили…

    Reply ↓
  38. Perfolenta

    так и не понял, удалось ли вам получить на ассемблере

    результат 50 095 301 248 058 391 139 327 916 261?

    Reply ↓
  39. starik-2005

    (38)

    так и не понял, удалось ли вам получить на ассемблере

    результат 50 095 301 248 058 391 139 327 916 261?

    Да, получилось. Только вывел в двоичной системе. В итоге на 128 бит все-равно вышло дольше, чем на 80 на С.

    00000000000000000000000000000000101000011101110111011100101010100011100100011000110110100011001110000111101010111011100011100101

    Вообще, если без вывода бинарного значения, то 0,017 секунд получается.

    ЗЫ: В общем С++ — читер, т.к. при компиляции с О3 он часть расчетов не делает — сворачивает. При компиляции без оптимизации 0,072 время, т.е. в 5 раз дольше.

    Reply ↓
  40. starik-2005

    (37) это у меня получилось отправить в онлайн-калькулятор ваши цифры ))

    Reply ↓
  41. Perfolenta

    (40) понял…

    Reply ↓
  42. Perfolenta

    (39) теоретически, расчеты с константами компилятор может проделать на этапе компиляции… когда-то, еще на Фортране, такое видел… процессоры тогда совсем слабенькие были, но программа с миллионами тяжелых циклов выполнилась мгновенно… мы удивились и дизассемблировали ее… а там просто готовый ответ выводился… все были в шоке… сейчас уже конечно не вспомню, что за компилятор фортрана был, но тогда впечатлило сильно… компилятор просто понял, что ни каких данных извне в программу не поступает и посчитал все заранее…

    Кстати, еще сильно влияет на результат метод измерения времени… встроенный в компьютер таймер интервалы менее 50 миллисекунд очень не надежно измеряет… только в тиках процессора более менее точно получается, да и то, зависит от реализации (мир теперь многопоточный)…

    Reply ↓
  43. Perfolenta

    (39) скажите, вы в личку заглядываете? Я вам там вопрос написал, если можно, ответьте парой слов… спасибо…

    Reply ↓
  44. starik-2005

    (43) я как бы живу в линуховом мире. Тут NET — это джава, но я ее не люблю, поэтому пишу на С++, тем более что у меня нет проблем с пониманием того, как работает самый низкий уровень.

    Reply ↓
  45. starik-2005
    Reply ↓
  46. Perfolenta

    (45) да, результат интересный, однако вы отлично подтвердили тезис, что на ассемблере еще сложнее сделать, но работает быстрее…. правда, современные ассемблеры тоже стали довольно дружелюбными, гораздо приятней, чем раньше…

    Reply ↓
  47. starik-2005

    (46)

    однако вы отлично подтвердили тезис

    Не совсем. Тут сложно было только разделить 128-битное целое на 10, ибо если частное не попадает в 64 бита, то система отваливается на оверфлоу, что странно… В итоге нашел в интернетах, как это делается))) Все как на 1С.

    Reply ↓
  48. Perfolenta

    (47) не понял… хотите сказать, что на ассемблере писать легко? будьте объективны… если кто-то посмотрит впервые на листинг вашей программы, то все что он сразу поймет это то, что есть два вложенных цикла… а вот что и зачем там гоняется по регистрам сразу не поймешь, надо сидеть и думать… так это еще совсем простой алгоритм… если бы на ассемблере писать было не сложно, то и другие языки не понадобились бы…

    слегка помогут комментарии в листинге, но это не слишком упростит восприятие программы, только понимание того, что и где происходит…

    Я, конечно, со времен КР580ВМ80, Z80 и i286, i386 на ассемблере больше не писал… уже навыки не те, забывается и от жизни отстал, но писал много и прекрасно знаю, что на ассемблере писать сложнее, чем на Си, на Си сложнее, чем на Бейсике и т.д.

    У ассемблера, как языка, есть только два достоинства, скорость и компактность бинарного кода… у языков высокого уровня достоинств гораздо больше, чем и обусловлен выбор большинства программистов…

    Reply ↓
  49. starik-2005

    (48)

    Я, конечно, со времен КР580ВМ80, Z80 и i286, i386 на ассемблере больше не писал… уже навыки не те, забывается и от жизни отстал, но писал много и прекрасно знаю, что на ассемблере писать сложнее, чем на Си, на Си сложнее, чем на Бейсике и т.д.

    Фактически первый — это тот же 8086 от intel’a. А я в свое время на К1801ВМ(1) писал — аналог процессоров DEC (СМ ЭВМ), Там я даже в машинном коде (8-битный код, типа 10001 = mov (1) R0 (00), R1 (01) , 20001 = CMP R0, R1, ну и т.д.) писал без труда. На Z80 уже машинный код был сложен, асм тоже там с трудностями переносимости в памяти, поэтому проще было на бейсике писать, но только если скорость не нужна. На интеловских процессорах после К1801ВМх было непросто, т.к. не все регистры могли служить операндами для всех команд — что-то только с аккумулятором (то же деление), косвенная адресация только через индексные регистры — да, нужно было в голове держать, что SI+BX можно было написать, а SI+DX — нет.

    Но тем не менее достаточно просто все на асме в том случае, если тебе известно, как в памяти представлен тот или иной тип данных, как ее там выделить, как освободить — ведь асм, по-сути, все это у ОС выбирал.

    Я в свое время достаточно большой проект делал на Borland Pascal, и там была интерфейсная часть (текстовый интерфейс + VESA 800*600*16 — давно это было, под MS DOS 6.22 RTL PM), которая была написана на асме чуть менее, чем вся (стек окон, рисование объектов интерфейса, выделение цветом текста при выводе (с 0х0 для перфикса цвета), …). С тех пор не считаю асм сложным языком (по крайней мере 16-битный вариант).

    Reply ↓
  50. starik-2005

    (48)

    У ассемблера, как языка, есть только два достоинства, скорость и компактность бинарного кода… у языков высокого уровня достоинств гораздо больше, чем и обусловлен выбор большинства программистов…

    Ну по поводу скорости — очень условно, т.к. с -О3 -flto и на С/С++ скомпилится очень быстрый код, который сам скопипастит столько раз твои add/adc/xchg, сколько надо ))) А вот по компактности — да, очень компактную программу можно получить (я под MS DOS делал вьювер PCX-файлов — вроде бы 250 байт был всего com-фвйлик).

    Reply ↓
  51. Толямба

    (18)

    А Питон судя по всему повышает разрядность чисел динамически по мере необходимости… мой язык считал в Net типе Decimal

    Так ты и в питоне можешь считать в Decimal

    Reply ↓
  52. Perfolenta

    (51) в данном случае основное сравнение было с 1с, поэтому я питону специально тип не указывал… код был почти 1 в 1…

    а в моем языке статическая типизация, поэтому пришлось указать Decimal…

    Reply ↓
  53. Perfolenta

    (49) да, у нас с вами ностальгическая вечеринка… 🙂 сегодня не каждый «айтишник» скажет что такое VESA… 🙂

    Reply ↓
  54. Perfolenta

    (50) по поводу скорости согласен, однако в ассемблере, как говорится, все в ваших руках, а не под капотом, как у плюсов…

    Reply ↓
  55. Perfolenta

    (44) да, жаль, с вашим опытом 1с-ника и знанием языков низкого уровня, может что и подсказали бы мне…

    Reply ↓
  56. starik-2005

    (55) если это не будет работать под *nix’ ами, то я даже посмотреть не смогу.

    Вообще, как-то с другом в школе еще писали транслятор. Т.е. он писал, а я ему делал механизм рассылки. Как раз на С все пилилось, а рассылку он вкомпилил с asm’а — дело было еще на УКНЦ в институте развития образования. И у нас бы все получилось, если бы не закон Мура)))

    Reply ↓
  57. Perfolenta

    (56) ясно… компилятор и ИДЕ пока только под виндой работают… а полученные программы и на линуксах запускаются, но это пока мало протестировано… есть надежда, что с переходом на Net Core 3 ситуация с кроссплатформенностью сильно улучшится…

    Reply ↓
  58. starik-2005

    (18)

    пруфов не нашел, хотя интернет забит статьями типа «почему Питон медленный»…

    Кстати, немного переписал на питоне код:

    for j in range(1, 100000):
a = b = 1;
for i in range(1,139):
a = a + b;
(a,b) = (b,a);

print(a);

    В итоге вот как-то так на моей рязани:

    $ time python 1.py

    50095301248058391139327916261

    real 0m1,904s

    user 0m1,900s

    sys 0m0,004s

    Reply ↓
  59. starik-2005

    Кстати, на 1С всего-то в 14,34 раз дольше, чем на питоне…

     т = ТекущаяУниверсальнаяДатаВМиллисекундах();
Для х = 1 по 100000 Цикл
а = 1;
б = 1;
для у = 2 по 139 Цикл
а = а + б;
д = а;
а = б;
б = д;
КонецЦикла;
КонецЦикла;
Сообщить(ТекущаяУниверсальнаяДатаВМиллисекундах() — т);
Сообщить(а);

    Показать

    В итоге:

    1С = 27 сек

    Python = 1.9 сек

    С++ = 0.016 сек

    Asm = 0.005 сек

    Т.е. асм в 3 раза быстрее С++, который в 100 раз быстрее, чем питон, который в 14 раз быстрее, чем 1С. Сейчас на PHP протестю )))

    Reply ↓
  60. starik-2005

    PHP в 6 раз быстрее питона, однако…

    $i = 100000;
while($i—) {
$a = $b = 1;
for($j = 1; $j < 139; $j++ ) {
$a = $a + $b;
$tmp = $a;
$a   = $b;
$b   = $tmp;
}
}
print($a);

    Показать

    $ time php 1.php

    5.0095301248058E+28

    real 0m0,321s

    user 0m0,317s

    sys 0m0,004s

    $ php -v

    PHP 7.2.19-0ubuntu0.18.04.1 (cli) (built: Jun 4 2019 14:48:12) ( NTS )

    Copyright © 1997-2018 The PHP Group

    Zend Engine v3.2.0, Copyright © 1998-2018 Zend Technologies

    with Zend OPcache v7.2.19-0ubuntu0.18.04.1, Copyright © 1999-2018, by Zend Technologies

    Reply ↓
  61. Perfolenta

    (58) да, это интересно… оказывается в питоне range быстрее, чем циклы while, почти в 1.6 раза… на моей машине 2.7 и 4.3 сек соответственно.

    в моем языке наоборот, циклы Пока почти на 30% быстрее… 🙂

    0.28 против 0.21

    у меня этот код вот так выглядит:

    Для j Из Ряд(2, 100000)
Перем a,b тип Число = 1
Для i Из Ряд(1,137)
a += b
Присвоить a,b = b,a
КонецЦикла
КонецЦикла
ВыводСтроки b

    Показать

    у меня в ряде верхний предел включительно, поэтому числа скорректированы, но результат тот же…

    Reply ↓
  62. starik-2005

    (61) а что у Вас за процессор? Просто интересно сравнить

    Reply ↓
  63. Perfolenta

    (62) Intel Core i5-7200U 2.5GHz + 16Gb оперативки

    Reply ↓
  64. starik-2005

    (63)

    i5-7200U

    А не пробовали асмовский код компильнуть? Там в заголовке нужно модель на виндовую поменять, чтобы в винде заработало. Просто интересно, на сколько 7200 быстрее моего рабочего 5500…

    Reply ↓
  65. Perfolenta

    (64) а каким компилятором асма вы пользуетесь?

    Reply ↓
  66. starik-2005

    (65) FASM, но и под NASM с небольшой модификацией можно скомпилить. Ну и вывод числа надо на INT 21H перепилить под винду.

    http://www.codenet.ru/progr/dos/dos_0017.php

    Reply ↓
  67. Perfolenta

    (60) в типе Double не считается 🙂

    Reply ↓
  68. starik-2005

    (61) оказалось, что можно еще быстрее (почти в два раза), при этом питон 2 быстрее чем питон 3 почти в полтора раза:

    for j in range(0, 100000):
a = b = 1;
for i in range(1,138):
(a,b) = (b + a,a);

print(a);
    time python 1.py

    50095301248058391139327916261

    real 0m1,167s

    user 0m1,167s

    sys 0m0,000s

    Reply ↓
  69. starik-2005

    (61) кстати, на тему скорости. Вот, оказывается, есть такой проект — pypy, который компилит Python через трансляцию в С и выполняет его. При таком раскладе PHP отдыхает:

    $ time pypy 1.py

    50095301248058391139327916261

    real 0m0,181s

    user 0m0,169s

    sys 0m0,012s

    Reply ↓
  70. Perfolenta

    (68) что-то наши с вами результаты вообще не коррелируют о каких бы языках не шла речь… видимо на линуксе и винде реализации интерпретаторов слишком различны… не только ведь процессор может быть виноват…

    в данном случае я получил на Питоне 3.5 предсказуемую экономию времени примерно на 20%, а вы пишете, что в 2 раза почти… а ведь мы экономим только одно чтение и одну запись локальной переменной… это не может дать в 2 раза…

    аналогичную экономию я получил и на своей перфоленте…

    кстати, на FASMе что-то у меня не заработал ваш код, а разбираться почему мне не захотелось… извините уж, но слишком давно я на ассме не писал и вряд ли уже буду… есть много не решенных других задач, жаль время тратить…

    Reply ↓
  71. starik-2005

    (70) странно, что не коррелируют. Но, на всякий случай, подведу итоги:

    1. На питоне 2.7 алгоритм с двумя присваиваниями 1.904 секунды.

    2. На нем же алгоритм с одним присваиванием 1.167 — это не в 2 раза, конечно, но и не 20%.

    3. На PyPy алгоритм с одним присваиванием 0.181.

    По поводу кода, то код ядра интерпретатора вряд ли пишется отдельно для винды и линуха — там лишь механизм взаимодействия с ОС в некоторой части отличается. Сам интерпретатор идентичен. Винда может память выделять иначе, но вряд ли это будет существенно влиять, т.к в этих алгоритмах память почти не используется — четыре переменные всего.

    ЗЫ: а по поводу ассемблера, то это лишь тест оставшихся способностей преодолевать сложность))) Я скину для винды код, ибо у меня есть семерка на виртуалке. Поглядим что там как)))

    Reply ↓
  72. Perfolenta

    (71) перетестировал еще раз на питоне 3.5.2: в первом случае 2.867 сек., во втором 2.325… у вас соотношение явно больше… почему, не понятно… в чем у вас такой выигрыш состоит, если число команд уменьшается не существенно?

    ОС вряд-ли тут может играть какую-либо роль… а реализация интерпретатора может…

    ЗЫ: способности преодолевать сложности у меня еще остались, а то я бы создание собственного языка программирования не ослил… а вот со временем жуткий напряг… и тут вряд ли я могу что-то поменять в ближайшее время…

    Reply ↓
  73. Perfolenta

    (71)

    у меня есть семерка на виртуалке

    ну вот, а говорили, что даже посмотреть мой язык не сможете, т.к. не на чем.. 🙂

    Reply ↓
  74. spacecraft

    (18) 

    n=139;
j = 0;
Пока j < 100000 Цикл
j = j + 1;
fib1 = 1;
fib2 = 1;
i = 0;
Пока i < n — 2 Цикл
fib_sum = fib1 + fib2;
fib1 = fib2;
fib2 = fib_sum;
i = i + 1;
КонецЦикла;
КонецЦикла;
Сообщить(fib2);

    Показать

    1С — 112 сек

    А теперь попробуйте тот же код в ином оформлении:

    т = ТекущаяУниверсальнаяДатаВМиллисекундах();
n=139;
j = 0;
Пока j < 100000 Цикл j = j + 1;fib1 = 1;fib2 = 1;i = 0;Пока i < n — 2 Цикл fib_sum = fib1 + fib2;fib1 = fib2;fib2 = fib_sum;i = i + 1;КонецЦикла;КонецЦикла;
Сообщить(ТекущаяУниверсальнаяДатаВМиллисекундах() — т);
Сообщить(fib2);

    Неожиданно? Да, 1С не хватает оптимизации, но не все так печально.

    Reply ↓
  75. starik-2005

    (74) если взять код из (59) и свернуть в одну строку, то получается 8 секунд. Это в 4 раза 6 раз медленнее питона всего (8,33 против 1,38). Уже не плохо, но код в итоге не читаем совершенно становится.

    Reply ↓
  76. spacecraft

    (75) Для конкретных таких мест, где требуется увеличение быстродействия, то вполне можно использовать. Рекомендовать использовать везде не буду, нет смысла.

    Reply ↓
  77. starik-2005

    (76) я, так понимаю, что это просто выпиленные из 1С-асма строки «linenum XX». На них как-то больно много 1С тратит — больше половины времени.

    Reply ↓
  78. spacecraft

    (77) я думаю, что можно использовать решение из этой темы и посмотреть что конкретно меняется в коде на низком уровне.

    Reply ↓
  79. spacecraft

    (78) из этой темы: https://infostart.ru/public/1080907/

    Reply ↓
  80. Perfolenta

    (74) 18 747 против 14 656 миллисекунд… лучше конечно, но не принципиально… всю программу в таком стиле не напишешь…

    вы, наверное, из конфигуратора под отладчиком запускали… поэтому у вас могла большая разница получиться…

    Reply ↓
  81. starik-2005

    (80)

    14 656 миллисекунд.

    Что-то долго у Вас. У меня на i7-5500U так:

    Reply ↓
  82. starik-2005

    (80) кстати, убрал пробелы — стало еще быстрее (это, кстати, на тему именования переменных — чем длиннее имя переменной, тем дольше работает 1С походу):

    Reply ↓
  83. spacecraft

    (80) сравниваете какие листинги кода? Сами же приводили время выполнения кода (18) 1С — 112 сек. Код в (74) который в одну строку 1С — 14 сек. Разница довольно ощутимая.

    Reply ↓
  84. Perfolenta

    (83) а, извиняюсь, значит это я прошлый раз лоханулся и под отладчиком запускал… сейчас: 18 747 против 14 656 миллисекунд… лучше конечно, но не принципиально…

    Reply ↓
  85. Perfolenta

    (81) да ваш i7-5500U намного быстрее моего i5-7200U это мы уже с вами не раз отметили…

    Reply ↓
  86. starik-2005

    (85)

    ваш i7-5500U намного быстрее моего i5-7200U

    Это мой Ryzen 1600 быстрее, а по поводу i5 с частотой 2,5-3,1, то вряд ли он будет медленнее чем i7 с частотой 2,4-3,0 )))

    Reply ↓
  87. Perfolenta

    (82) а вот этого я вообще не понимаю… в теории байткод как раз и делается для того, что бы ни пробелы, ни длина имен не влияли на выполнение программы…

    ладно, еще можно понять, когда в одну строку быстрее работает, да и то с трудом (метка строки по идее должна просто пропускаться)…

    Reply ↓
  88. starik-2005

    (87)

    а вот этого я вообще не понимаю

    Я тоже (первый вариант — в одну строку, второй — в несколько):

    ЗЫ: исходники в теме про асм.

    Reply ↓
  89. Perfolenta

    (88) странно, у меня, как и в случае с питоном, разница значительно меньше получается… что мы с вами не так делаем?

    Reply ↓
  90. Perfolenta

    (86) ну не знаю… сейчас запустил вашу обработку FIB.epf и получил 9 644, т.е. близко к вашему результату… но все равно на секунду медленнее…

    сравнил код… у вас все в одну строку, а у меня только циклы были в одну строку… и уже давало 14 656… это не 1с, а ребус какой-то… 🙂

    Reply ↓
  91. starik-2005

    (90) дома на 1600-м райзене попробовал:

    8 102

    50 095 301 248 058 391 139 327 916 261

    8 110

    50 095 301 248 058 391 139 327 916 261

    8 125

    50 095 301 248 058 391 139 327 916 261

    12 743

    50 095 301 248 058 391 139 327 916 261

    12 682

    50 095 301 248 058 391 139 327 916 261

    12 659

    50 095 301 248 058 391 139 327 916 261

    В принципе видимо на работе действительно дебагер не выключен был, но тем не менее разница ощутима в одну строку и в несколько…

    Reply ↓
  92. muskul

    Для вычисления диаметра вселенной с точностью до атома достаточно всего 63 знака после запятой

    Reply ↓
  93. starik-2005

    (92)

    с точностью до атома

    Чета хренова точность, с учетом того, что в теории Инфляции первоначальная точка была типа размером 1*10-93, что уже 93 разряда до запятой )))

    Reply ↓

Leave a Comment

Ваш адрес email не будет опубликован. Обязательные поля помечены *