Начиная с версии платформы 8.3.14.1565 в 1С:Предприятие стал доступен объект для решения системы линейных уравнений. Следует предположить, что данный функционал не вызвал значительного интереса, так как я не нашел на infostart ни одного упоминания, относящегося к данному предмету. Поиск через Яндекс вывел на статью "Механизм решения систем линейных алгебраических уравнений", которая всем хороша, за исключением того, что не содержит примера применения нового класса РасчетСистемЛинейныхУравнений. Этот пробел я и постараюсь восполнить. Решать будем систему из трех уравнений, которая вынесена в заголовок статьи.
x -3y+5z =-10
2x + y — z =5
4x+2y+3z =5
На первом шаге подготовим две таблицы значений. В одной будем хранить коэффициенты из левой части, а в другой свободные члены системы уравнений.
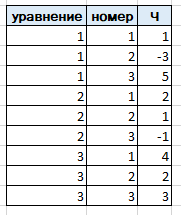
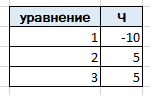
Каждая из таблиц содержит колонку уравнение, в которой указывается номер уравнения , а так же колонку Ч, в которую заносятся значения коэффициентов. Кроме этого, таблица с коэффициентами из левой части решаемой системы содержит колонку номер, для указания номера переменной, к которой относится данный коэффициент. Упростим себе жизнь и и напишем две процедуры для заполнения данных таблиц.
//-----------------------------------------------------------------
// куда - таблица значений, в которую добавляются свободные члены
// что - строка со значениями коэффициентов из правой части уравнения,
// которые разделены ';'
Функция ДобавитьСвободныеЧлены(куда,что)
данные=СтрРазделить(что,";",ЛОЖЬ);
инд=1;
для каждого к из данные цикл
запись=куда.Добавить();
запись.уравнение=инд ;
инд=инд+1 ;
запись.Ч=число(к) ;
конеццикла;
возврат куда;
КонецФункции
//--------------------------------------------------------------------------------------------
// куда - таблица значений, в которую добавляются коэффициенты уравнения из левой части
// что - строка со значениями коэффициентов,которые разделены ';'
// номер_уравнения - номер уравнения, которому относятся коэффициенты
Функция ДобавитьКоэффициенты(куда,что,номер_уравнения)
данные=СтрРазделить(что,";",ЛОЖЬ);
инд=1;
для каждого к из данные цикл
запись=куда.Добавить() ;
запись.уравнение=номер_уравнения ;
запись.номер=инд ;
инд=инд+1 ;
запись.Ч=число(к) ;
конеццикла;
возврат куда;
КонецФункции
Теперь выполним подготовительные процедуры.
ТипЧисло=новый ОписаниеТипов("Число");
СвободныеЧлены=новый ТаблицаЗначений ;
СвободныеЧлены.Колонки.Добавить("уравнение",ТипЧисло) ;
СвободныеЧлены.Колонки.Добавить("Ч",ТипЧисло) ;
//заносим в таблицу значения свободных членов
ДобавитьСвободныеЧлены(СвободныеЧлены,"-10;5;5") ;
Коэффициенты=новый ТаблицаЗначений ;
Коэффициенты.Колонки.Добавить("уравнение",ТипЧисло);
Коэффициенты.Колонки.Добавить("номер",ТипЧисло) ;
Коэффициенты.Колонки.Добавить("Ч",ТипЧисло) ;
//заносим значения коэффициентов из левой части
ДобавитьКоэффициенты(Коэффициенты,"1;-3;5",1) ;
ДобавитьКоэффициенты(Коэффициенты,"2;1;-1",2) ;
ДобавитьКоэффициенты(Коэффициенты,"4;2;3",3) ;
На следующем шаге переходим к работе с объектом РасчетСистемЛинейныхУравнений. У него есть два свойства, первое — ИсточникДанныхУзлов, через которое передаются значения свободных коэффициентов, и свойство ИсточникДанныхСвязей для передачи значений коэффициентов из левой части системы линейных уравнений. Отметим, что кроме сформированных таблиц мы указываем имена колонок, в которых хранится номер уравнения и номер переменной.
Расчет=новый РасчетСистемЛинейныхУравнений ;
//коэффициенты из левой части уравнения
Расчет.ИсточникДанныхСвязей=Коэффициенты ;
Расчет.КолонкаУравненияВСвязях ="уравнение" ;
Расчет.КолонкаПеременныеВСвязях="номер" ;
//коэффициенты из правой части уравнения
Расчет.ИсточникДанныхУзлов=СвободныеЧлены ;
Расчет.КолонкаУравненияВУзлах="уравнение" ;
Заключительный штрих. Для того чтобы все заработало надо добавить ОписанияСистемЛинейныхУравнений в коллекцию ОписанияСистем класса РасчетСистемЛинейныхУравнений.
описание=Расчет.ОписанияСистем.Добавить();
описание.КолонкаКоэффициентовВСвязях="Ч" ;
описание.КолонкаКоэффициентовВУзлах ="Ч" ;
И наконец непосредственный расчет.
ответ=Расчет.РассчитатьСистемыЛинейныхУравнений() ;
для каждого запись из ответ цикл
сообщить(запись.Решение1);
конеццикла;
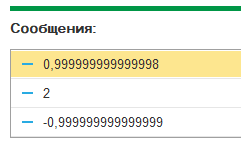
Точное решение для данной системы :
x=1;
y=2;
z=-1
Убедиться в этом можно непосредственной подстановкой. Программа дает ответ с некоторой точностью, что обусловлено применяемым итерационным алгоритмом.
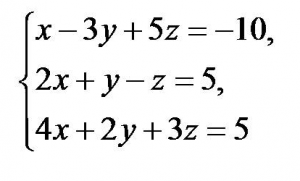




А вот бы еще пояснили на простом примере как расчет системы линейных уравнений используется при расчете себестоимости в РАУЗ.
(1)
Минус за корявый код!
Также уравнение написали бы текстом.
Дополнительно не понятно, а где ответы?
1 — 6 — 5 = -10 в целом сходится, но это же надо еще посчитать.
Дооформите, чтобы глаза не резало!
Механизм был бы классный, если бы они использовали другой метод для расчета СЛАУ.
У метода простых итераций слишком серьезные минусы и использование его в финансовых системах — очень сомнительная идея.
Что и показывает ваш простенький пример — вместо 1, получили 0,(9).
Да, и в РАУЗе используется тот-же метод, но не уверен, что расчет идет через данный объект.
А представление СЛАУ в табличном виде, все-таки, лучше в матричном виде делать.
(4)В УПП не будет типовой поддержки этого класса. в ERP 2.х скорее всего появится в этом году (ближе к зиме).
(4) Вообще-то они на хабре обосновывали зачем придумали свой метод решения, он как раз быстрее стандартных именно в финансовых системах — на разреженных больших матрицах
(6) Он быстрее только за счет того, что они забили на контроль вырожденности матрицы.
А это в свою очередь приводит к бредовым цифрам, если в исходных данных что-то не так. И эти цифры еще надо обнаружить. Когда появился РАУЗ очень многие этому удивлялись, но в 1С, видимо, решили что оно так лучшее. Зато у программистов на сопровождении всегда есть работа.
(7) Тут по результатам попытки использования РАУЗ в розничной сети. В вкратце, из-за постоянного пересорта товаров в магазинах и, как следствие, отрицательные остатки до проведения инвентаризации, все основные отчеты приходили в полную негодность после расчета себестоимости (триллионы в списанной себестоимости на оборотке и в типовых отчетах). Причем как повезет, иногда ошибка с отрицательным остатком не приводит к постоянному увеличению отклонения, а иногда приводит. Но так как ассортимент большой и магазинов было под 50, ситуация с некорректным расчетом возникала постоянно. А постоянные пересорты и отрицательные остатки в рознице — это данность с которой ничего не сделать.