Чем хороша математика? Возможно, тем, что с помощью универсального языка формулирует методы и решения, которые впоследствии можно применять к самым разным явлениям окружающего мира. Задача разработчика состоит в том, чтобы за различными формами разглядеть общее содержание и эффективно использовать разработанный для этого содержания математический аппарат. Проиллюстрируем данный тезис с помощью статей, которые были в разное время размещены на портале infostart.
Начнем с "ФИФО для любопытных". В данной публикации обсуждается, как одним запросом получить все движения расходных документов за период. Есть таблица приходных накладных, которые формируют партии товаров, и таблица расходных накладных, в которых эти товары списываются. Необходимо для каждого документа списания указать документы партии и количество товара, которое списывается с каждой партии. Теперь обратимся к "Распределение в запросе" или "избавляемся от перебора". Автор приводит найденное им решение для следующей задачи. Есть складские ячейки с известной емкостью (A, B, C, D) и сам товар (X, Y, Z), который необходимо «как-то» разложить по этим ячейкам, но так, чтоб в ячейку не положили больше товара, чем может быть в ней места.
При всей ,на первый взгляд,непохожести обсуждаемых в данных статьях темах речь идет об одной и той же математической задаче. Есть два множества отрезков. Отрезки заданы координатами начала и конца, причем координаты правой точки больше координаты левой. Каждому отрезку сопоставлен уникальный индекс,например ссылка на документ. Надо определить какие отрезки пересекаются и вычислить длину этого пересечения. Покажем как формируются эти отрезки. Рассмотрим задачу "Ячейки и Товары".
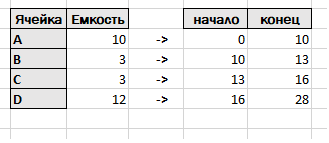
Таблица с ячейками переходит в таблицу с отрезками, где начало и конец определяются с помощью запроса с нарастающими итогами. Аналогично строим таблицу для товаров.
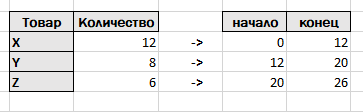
Понятно, что если поменять местами строчки в каждой таблице, то поменяются значения в колонках начало и конец. На числовой прямой отрезки будут выглядеть следующим образом.
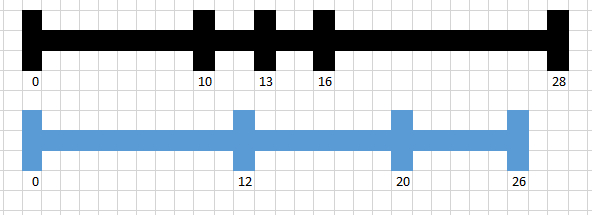
Найдем критерий, по которому мы можем собрать пересекающиеся отрезки. Эта задача решена древними греками, а может и еще раньше. Приведем одно из возможных рассуждений. Даны два отрезка А(начало,конец) и Б(начало,конец). Начало и конец это координаты отрезка. Проще всего сформулировать правило , при котором отрезки НЕ пересекаются. Оно такое (А.конец < Б.начало ИЛИ A.начало>Б.конец). Применим к данному выражению отрицание, тогда оно трансформируется в условие (А.конец>= Б.начало И A.начало<=Б.конец). После этого становится понятно, как выбрать все пары пересекающихся отрезков.
Текст="ВЫБРАТЬ
| А.индекс КАК Аи,
| Б.индекс КАК Би
|ИЗ
| А КАК А
| ВНУТРЕННЕЕ СОЕДИНЕНИЕ Б КАК Б
| ПО А.конец >= Б.начало
| И А.начало <= Б.конец";
Теперь осталось добавить длину пересечения. А она равна Мин(А.конец,Б.конец)-Макс(А.начало,Б.начало), что на языке запросов выглядит как:
Текст="ВЫБРАТЬ
| А.индекс КАК Аи,
| Б.индекс КАК Би,
| ВЫБОР
| КОГДА А.конец < Б.конец
| ТОГДА А.конец
| ИНАЧЕ Б.конец
| КОНЕЦ - ВЫБОР
| КОГДА А.начало > Б.начало
| ТОГДА А.начало
| ИНАЧЕ Б.начало
| КОНЕЦ КАК Пересечение
|ИЗ
| А КАК А
| ВНУТРЕННЕЕ СОЕДИНЕНИЕ Б КАК Б
| ПО А.конец >= Б.начало
| И А.начало <= Б.конец";
Применим предложенный алгоритм к нашим данным.
Функция ДобавитьОтрезок(длина,куда)
запись =куда.Добавить() ;
запись.индекс =куда.Количество();
если запись.индекс=1 тогда
запись.начало =0 ;
иначе
запись.начало =куда[запись.индекс-2].конец;
конецесли;
запись.конец =запись.начало+длина;
возврат запись;
КонецФункции
Функция Пересечение() export
start=ТекущаяУниверсальнаяДатаВМиллисекундах();
типЧ=новый ОписаниеТипов("Число");
тзА = new ТаблицаЗначений;
тзА.Колонки.Добавить("индекс",типЧ);
тзА.Колонки.Добавить("начало",типЧ);
тзА.Колонки.Добавить("конец",типЧ);
ДобавитьОтрезок(10,тзА);
ДобавитьОтрезок(3 ,тзА);
ДобавитьОтрезок(3 ,тзА);
ДобавитьОтрезок(13,тзА);
тзБ = тзА.СкопироватьКолонки();
ДобавитьОтрезок(12,тзБ);
ДобавитьОтрезок(8 ,тзБ);
ДобавитьОтрезок(6 ,тзБ);
Текст="ВЫБРАТЬ
| тз.индекс КАК индекс,
| тз.начало КАК начало,
| тз.конец КАК конец
|ПОМЕСТИТЬ А
|ИЗ
| &тзА КАК тз
|;
|
|////////////////////////////////////////////////////////////////////////////////
|ВЫБРАТЬ
| тз.индекс КАК индекс,
| тз.начало КАК начало,
| тз.конец КАК конец
|ПОМЕСТИТЬ Б
|ИЗ
| &тзБ КАК тз
|;
|
|////////////////////////////////////////////////////////////////////////////////
|ВЫБРАТЬ
| А.индекс КАК Аи,
| Б.индекс КАК Би,
| ВЫБОР
| КОГДА А.конец < Б.конец
| ТОГДА А.конец
| ИНАЧЕ Б.конец
| КОНЕЦ - ВЫБОР
| КОГДА А.начало > Б.начало
| ТОГДА А.начало
| ИНАЧЕ Б.начало
| КОНЕЦ КАК Пересечение
|ИЗ
| А КАК А
| ВНУТРЕННЕЕ СОЕДИНЕНИЕ Б КАК Б
| ПО А.конец >= Б.начало
| И А.начало <= Б.конец";
запрос=новый запрос(Текст);
запрос.Параметры.Вставить("тзА",тзА);
запрос.Параметры.Вставить("тзБ",тзБ);
ответ=запрос.Выполнить().Выгрузить();
end=ТекущаяУниверсальнаяДатаВМиллисекундах();
message("выполнение запроса "+(end-start));
возврат ответ;
КонецФункции
Функция ДобавитьОтрезок добавляет отрезок в массив, функция Пересечение возвращает пересечение отрезков из приведенного выше примера.
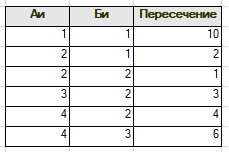
Именно этот алгоритм и реализован в приведенных выше публикациях. Можно ли предложить более эффективное решение. Да, можно, и вот почему. Приведенный запрос будет правильно работать для любых наборов отрезков, в том числе и пересекающихся внутри одного множества. В тоже время, по условиям задачи отрезки расположены непрерывно на числовой прямой,не пересекаются и конец предыдущего совпадает с началом следующего (спасибо нарастающим итогам).
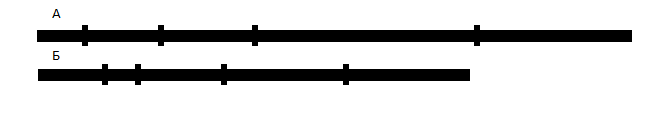
В этом случае мы можем заменить представление отрезка его длиной и порядком следования(индексом) А[индекс](длина). Индекс — это номер отрезка в таблице, длина — колонка из таблицы, в которой хранятся рассматриваемые отрезки. Рассмотрим два левых отрезка А и Б. Они пересекаются и длина пересечения равна длине минимального из них. Уберем этот отрезок из множества, в которое он входит, а второй укоротим на длину пересечения. Повторим нашу процедуру. Остановимся, когда обработаем все отрезки в первом или втором множестве. Именно такой алгоритм предложил Сергей в публикации "Минимализмы" раздел 7. Связывание таблиц значений по ФИФО. Кстати, частным случаем данного алгоритма является списание по партии внутри одного расходного документа, что вполне естественно. Предложенный алгоритм показывает значительный выигрыш в быстродействии по сравнению с запросом, поскольку учитывает особенность расположения отрезков в исходных множествах.
Надеюсь, что данная статья будет полезна при поиске общих математических подходов для непохожих, в первом приближении, процессов.
Related Posts
Получение логина и пароля техподдержки 1С из базы
Класс для вывода отчета в Excel
Счет-фактура для УПП
Библиотека классов для создания внешней компоненты 1С на C#- Акт об оказании услуг (со скидками) — внешняя печатная форма для Управление торговлей 11.1.10.86
Прайс-лист с артикулом в отдельной колонке
Очень полезная информация.Спасибо.
Вот шайтан. Пожалуйста добавьте в эту статью примеров с цифрами. Очень хочу в этом разобраться но никак не «въеду».
«Предложенный алгоритм показывает значительный выигрыш в быстродействии по сравнению с запросом»
Ну, я думаю, и этот алгоритм можно запросом оформить, но нужно ли ? ildarovich бы точно смог 🙂
(3)Думаю, что запросом это не сделать. Иначе бы ildarovich это сделал, а он предложил решение через программный код.
В первоначальном варианте статьи была ошибка в запросе — сравнение индексов. Оно требуется, если ищутся пересекающиеся отрезки внутри одного множества. Когда работаем с двумя множествами, надо соединить «каждый с каждым» и это сравнение будет ошибкой.
Прочитал бегло статью — ничего не понял, но тема заманчивая. Почитал статьи по ссылкам.
Первая статья сводится к мысли: «вот если бы не было регистров накопления, тогда я бы выкрутился вот так».
Вторая статья, выдвигает тезис: «перебор всегда хуже чем запрос», довольно странное утверждение, т.к. запрос будет преобразован в план выполнения запроса, а там уже тот самый перебор, который хуже чем запрос. Понятно, что в одном случае выборки выполняются интерпритатором 1С, в другом случае скомпилированный код, но неужто прямо такие гигантские потери? В обсуждении статьи все прекрасно разобрано, в т.ч. про утверждения о великолепии использования хитровывернутых запросов.
Это же язык запросов, нам не надо задумываться как будут получены данные, нам главное написать запрос, север SQL сам разберется как лучше. Лично убеждался, даже на относительно простых запросах может и не разобраться, причем самое приятное, что в одном случае результат запроса будет формироваться мгновенно, а в другом случае тот же самый запрос будет выполняться несколько минут.
Можно использовать критерий квадратного трехчлена — если х лежит в интервале х2, х3, то (х-х2)(х-х3)<0
(3) (4) Слежу за этой темой. Сейчас есть вот такие мысли. Привожу их больше для желания собрать свой «state of art» по этой теме.
Запросом у меня есть: . Как раз из комментариев к статье , которая здесь упомянута. Просто более аккуратное, на мой взгляд решение, но не более быстрое.
Теперь, если нужно более быстрое решение для пересечения отрезков параллельных прямых при проецировании на одну прямую.
Здесь два пути:
исторически первый — дискретизация интервалов путем деления на наименьший интервал, чтобы затем определить общие куски группировкой. Это решает проблему квадратичной зависимости роста времени выполнения запроса от числа отрезков. Этот путь я планировал для быстрого ФИФО запросом.
Второй путь был найден позднее в статье . На нем тоже можно основать быстрый запрос линейный по скорости. И он «красивее».
В общем алгоритме быстрого ФИФО запросом есть еще задача нахождения нарастающего итога.
Пока я искал (и нашел) способ «Баттерфляй» без предварительной нумерации, в запросах нумерация строк появилась (!!!). Это требует пересмотра многих ранее написанных запросов, которые с нумерацией решаются линейно по скорости.
Еще в несколько раз ускорить метод Баттерфляй позволяет экономия на записи во временные таблицы. Вывел формулу определения эффективных делителей в , зависящую от соотношения затрат на запись и чтение.
Но все это осталось в черновиках, потому что явного большого интереса к выполнению таких вычислений именно в запросе я не увидел. К тому же нужно посмотреть как будет на этих задачах работать новая разработка 1С «Ускоритель аналитических запросов».
(8)
На какой версии платформы ?
(9) 8.3.13, функция называется АВТОНОМЕРЗАПИСИ()
Вроде понятно, но перечитал еще раз и стало непонятно:)
Откуда у нас координаты каждого отрезка, чтобы писать такие условия? У нас есть только индекс отрезка (дата документа) и длина отрезка (количество товара). Ни начала ни конца у нас нет
Для того, чтобы понять координаты начала и конца отрезков текущих остатков нам надо узнать длины предыдущих, которые мы списали 10 лет назад, т.е. вытянуть в запрос всю историю данного товара от начала ведения базы по приходам и расходам, а это уже такое себе решение.
Или я что-то не уловил? Ткните в меня своей мыслью еще раз, очень интересно.
(11) Добавил в статью пример для задачи Ячейки и Товары. Для списания по партиям аналогично. Получаем остатки по партиям на начальную дату, добавляем в список приходы. Это первое множество. Второе множество получаем из расходных накладных.
(12) ну т.е. получаем срез на какую-то дату обычным способом из регистра накопления, а от него уже отрезками. Понял
Хотел бы отметить, что получать последовательности отрезков можно и запросом.
Показать
И да, АВТОНОМЕРЗАПИСИ() позволяет весь пример сделать запросом без кода.
(14) Текст запроса неправильный, КонОстаток считает неправильно.