Простая и быстрая хэш функция (hash) средствами 1С (оптимизированный вариант)

16.05.2017 16 Comments

Практика программирования, Разработка

    Замеры производительности
Данная функция основана на разработке "Простая и быстрая хэш функция (hash) средствами 1С" http://infostart.ru/public/70030/
Главное отличие от оригинальной функции — оптимизация по быстродействию для больших объемов исходных данных. По результатам замеров количества генерируемых хэшей в минуту на строке длиной 1222 символа:

Оригинальная функция: 14880
Оптимизированная функция: 21528

(т.е. +45%)

В оригинальной функции исходная строка разбивается на блоки (по 10 символов). Затем в цикле выбираем последовательно все символы из блока, и код этого символа используем при вычислении хэш функции.

Суть оптимизации достаточно проста — вместо цикла по символам из блока, в одной «большой и сложной формуле» 🙂 вычислить один раз хэш функцию для этого блока. Т.е. использовать в ней сразу же и первый, и второй и т.д. символы.

На строке в пару десятков символов оригинальная функция конечно, быстрее. А вот наглядный пример, где на входе строка длиной 1222 символа (результат оптимизированной функции выделен красным):

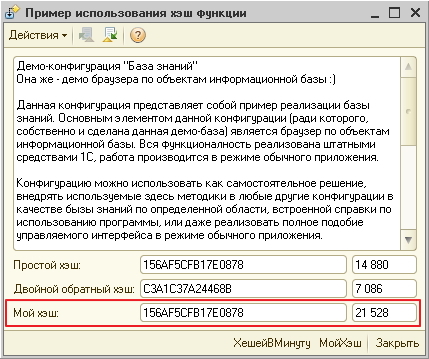
Замер производительности

Где именно находится граница, после которой оптимизированный вариант начинает работать быстрее оригинального, я не проверял (думаю, это может вызывать чисто академический интерес). Все замеры производились на строках более килобайта.

Почему было сделано именно так? Потому что на небольших объемах данных даже более медленная в несколько раз функция отработает за ничтожно малый промежуток времени. А сокращение времени обработки большого файла — это уже серьезно (при тестах использовался jpeg файл объемом 242КБ (333КБ после преобразования в строку Base64). Какие-то проценты производительности можно выжимать и далее, но пока решено остановиться на достигнутом.

Из прочих оптимизаций по мелочи — используется длина блока 11 символов (вместо 10), и добавлена возможность принимать в качестве исходных данных двомичные данные.

Функция глХэш(ИсходныеДанные, Хэш=5381, М=33, Разрядность=18446744073709551616)

    // приведем к строке
    Если ТипЗнч(ИсходныеДанные) = Тип(«ДвоичныеДанные») Тогда
        СтрокаДляКодирования = Base64Строка(ИсходныеДанные);
    Иначе
        СтрокаДляКодирования = Строка(ИсходныеДанные);
    КонецЕсли;

    ДлинаБлока = 11;
    НачПозиция = 1;
    ДлинаСтроки = СтрДлина(СтрокаДляКодирования);

    Пока НачПозиция <= ДлинаСтроки Цикл
        СтрокаБлока = Сред(СтрокаДляКодирования, НачПозиция, ДлинаБлока);
        ДлинаПодстроки = СтрДлина(СтрокаБлока);
        Если ДлинаПодстроки = ДлинаБлока Тогда
            Хэш = ((((((((((( Хэш*М + КодСимвола(СтрокаБлока, 1))*М + КодСимвола(СтрокаБлока, 2))*М
                + КодСимвола(СтрокаБлока, 3))*М + КодСимвола(СтрокаБлока, 4))*М + КодСимвола(СтрокаБлока, 5))*М
                + КодСимвола(СтрокаБлока, 6))*М + КодСимвола(СтрокаБлока, 7))*М + КодСимвола(СтрокаБлока, 8))*М
                + КодСимвола(СтрокаБлока, 9))*М + КодСимвола(СтрокаБлока, 10))*М + КодСимвола(СтрокаБлока, 11))
        Иначе
            Для к = 1 По ДлинаПодстроки Цикл
                Хэш = М * Хэш + КодСимвола(СтрокаБлока, к)
            КонецЦикла
        КонецЕсли;
        Хэш = Хэш % Разрядность;
        НачПозиция = НачПозиция + ДлинаБлока
    КонецЦикла;

    Возврат Хэш;

КонецФункции

Код для 7.7:

Функция глХэш(ИсходныеДанные, Хэш=5381, М=33, Разрядность=18446744073709551616)

    СтрокаДляКодирования = Строка(ИсходныеДанные);

    ДлинаБлока = 11;
    НачПозиция = 1;
    ДлинаСтроки = СтрДлина(СтрокаДляКодирования);

    Пока НачПозиция <= ДлинаСтроки Цикл
        СтрокаБлока = Сред(СтрокаДляКодирования, НачПозиция, ДлинаБлока);
        ДлинаПодстроки = СтрДлина(СтрокаБлока);
        Если ДлинаПодстроки = ДлинаБлока Тогда
            Хэш = ((((((((((( Хэш*М + КодСимв(Сред(СтрокаБлока, 1, 1)))*М + КодСимв(Сред(СтрокаБлока, 2, 1)))*М
                + КодСимв(Сред(СтрокаБлока, 3, 1)))*М + КодСимв(Сред(СтрокаБлока, 4, 1)))*М + КодСимв(Сред(СтрокаБлока, 5, 1)))*М
                + КодСимв(Сред(СтрокаБлока, 6, 1)))*М + КодСимв(Сред(СтрокаБлока, 7, 1)))*М + КодСимв(Сред(СтрокаБлока, 8, 1)))*М
                + КодСимв(Сред(СтрокаБлока, 9, 1)))*М + КодСимв(Сред(СтрокаБлока, 10, 1)))*М + КодСимв(Сред(СтрокаБлока, 11, 1)))
        Иначе
            Для к = 1 По ДлинаПодстроки Цикл
                Хэш = М * Хэш + КодСимв(Сред(СтрокаБлока, к, 1))
            КонецЦикла
        КонецЕсли;
        Хэш = Хэш % Разрядность;
        НачПозиция = НачПозиция + ДлинаБлока
    КонецЦикла;

    Возврат Хэш;

КонецФункции

(Для 7.7 не проводились замеры, чтобы определить оптимальный размер блока)

Не претендует на безошибочность и абсолютное чемпионство в быстродействии. Но если кому-нибудь пригодится — буду рад.

Пример использования — см. в прилагаемом файле. Также в данном виде функция использовалась в разработке «База знаний (демо-конфигурация браузера по объектам информационной базы)» //infostart.ru/public/100636/

Related Posts

16 Comments

  1. tormozit

    Спасибо.

    Интересно, каков самый быстрый способ вычислить хэш структуры без учета порядка элементов.

    Ниже в примере внутреннее представление структур будет различным и хэши этих представлений следовательно тоже.

    А = Новый Структура;
А.Вставить(«к1»);
А.Вставить(«к2»);
Сообщить(ЗначениеВСтрокуВнутр(А));

А = Новый Структура;
А.Вставить(«к2»);
А.Вставить(«к1»);
Сообщить(ЗначениеВСтрокуВнутр(А));

    Показать

    Самое первое что приходит в голову — обходить структуру и засовывать ее в список значений, затем его сортировать и затем уже получать представление.

    Но может быть кто то нашел более эффективный способ?

    Reply ↓
  2. Foxx

    (1) Поручик, да, таких функций в 7.7 нет 🙂

    Я думал, что приведенного кода вполне достаточно для его трансляции на платформу 7.7, ведь менять там почти ничего и не нужно. Но раз пошла такая пляска, добавил код и пример для 7.7.

    Reply ↓
  3. Foxx

    (2) tormozit, боюсь, без выгрузки в промежуточную коллекцию значений не обойтись.

    Еще, можно попробовать подобрать хэш-функцию, результат которой будет независим от последовательности исходных данных.

    Reply ↓
  4. Murom

    Интересная реализация.

    Но почему бы не использовать встроенные в Windows CAPI.

    HashData = Новый COMОбъект(«CAPICOM.HashedData»);
HashData.Algorithm = 1;  //Secure Hash Algorithm (SHA) that generates a 160-bit message digest.
HashData.Hash(тзСтрока.Наименование);

    Очень удобно тем что можно выбирать разные алгоритмы хешей. Притом «стандартные» и потом можно проверять в других сторонних (не 1с) программах.

    Reply ↓
  5. Поручик

    (5) COMОбъект’ы и ВК не всегда подходят.

    Reply ↓
  6. speshuric

    (0) Блочный вариант и в комментах к той статье был.

    (5) CAPICOM нужно ставить отдельно, есть проблемы с использованием в 64-битной среде, не предполагается дальнейшая поддержка от MS, не работает на линуксовом сервере, не работает в веб-клиенте.

    Reply ↓
  7. sergch2005

    Хорошая обработка. Давно искал.

    Reply ↓
  8. Foxx
    speshuric пишет:

    Блочный вариант и в комментах к той статье был.

    Был. Но он обладает несколькими недостатками — значительно меньшим быстродействием по сравнению с оригинальной функцией (учитывая оптимизации от alexk-is), независимо от объема исходных данных. И самое главное — он реализует другую хэш функцию, т.е. его нельзя использовать как замену оригинальной функции.

    Reply ↓
  9. speshuric

    (9) Я говорю про комментарий 31. Только что проверил. Изменив только способ передачи хеша. Передал строку длиной 6400 строк, результат одинаковый, производительность той, что в комментарии немного выше. ЧЯДНТ?

    Reply ↓
  10. Foxx

    (10) Прошу прощения, про другую функцию я немного погорячился.

    Правильнее будет выразиться так — упомянутая функция из 31 комментария выдает другой результат, если ее использовать «1 в 1» в том виде, как она приведена в комментарии.

    Оригинальная функция (во внешней обработке в демо-примере) и моя функция (со значениями по умолчанию) используют основание 33 и начальное значение хэша 5381 (функция Бернштайна). Функция из 31 поста — использует основание 31 и начальное значение 0 (функция Кернигана и Ритчи). Причем, без возможности изменения нач. значения хэша, т.к. инициализируется в коде самой функции, а не передается в качестве параметра.

    Если немного поправить код, то «функцию из 31 коммента» можно, конечно, заставить выдавать тот же самый результат :).

    Про скорость. Также должен принести извинения, порывшись в исходниках обнаружил, что для «функции из 31 коммента» я делал замеры без предварительной записи ее кода в одну строку. В таком виде она будет быстрее оригинальной. Но тем не менее, медленнее моего варианта). Сделал только-что замер на компьютере, который сейчас под рукой (6400 символов):

    Оригинальная функция: 1806 хэшей в минуту

    «функция из 31 коммента» (с записью кода в одну строку): 2316

    моя функция: 2424

    Reply ↓
  11. speshuric
    Reply ↓
  12. Foxx
    Да, ваш вариант быстрее на 1,5-2 процента в «боевом режиме» (как 8.1, так и 8.2)

    Мда, негусто. Ради такого результата не стоило и отдельную статью публиковать, достаточно было в предыдущей публикации в комментариях отписаться. (ух, как я прошляпил на первоначальных замерах у себя…) Ну да ладно, удалять уже не буду, хоть несколько процентов, а все равно прирост).

    Reply ↓
  13. speshuric

    (13) Да ладно, всё равно же быстрее. Кстати, надо будет на досуге построить графики зависимости от длины строк в итерациях в секунду и мегабайтах в секунду. Хотя бы чтоб знать предел возможностей интерпретатора.

    Reply ↓
  14. gosizo

    спасибо за статью

    Reply ↓
  15. serg_gres

    (13) не хочу углубляться в теорию.

    Подскажите: насколько устойчив используемый Вами метод хэширования к коллизиям?

    Есть задача хэшировать документы (все реквизиты будут преобразовываться в строку), и отслеживать их изменения.

    Используемый алгоритм подойдет?

    Reply ↓
  16. Foxx

    (18) serg_gres, гарантий полного отсутствия коллизий вам конечно никто не даст)

    Для вашей задачи, я думаю, алгоритм вполне подойдет.

    Чтобы не быть совсем уж голословным:

    К-во коллизий для разных хэш функций в зависимости от разрядности таблицы:



    У меня используется функция Бернштайна (см. серую кривую) и 64-разрядный ключ (в графике ограничились 28-ю разрядами :))

    Оценка качества разных функций по формуле Red Dragon Book



    У нас кодируется UTF-8 текст (отмечено светло-голубым цветом). Как наглядно видно, функция Бернштайна вполне вписывается в «идеал» (диапазон 0.95-1.05) для всех исходников, кроме числовых.

    Reply ↓

Leave a Comment

Ваш адрес email не будет опубликован. Обязательные поля помечены *